MCMC Diagnostics

Example MCMC diagnostics with bbr.bayes.

bbr
model management

Introduction

In this expo, we make the distinction between two types of diagnostics:

  • Markov Chain Monte Carlo (MCMC) convergence diagnostics
  • Model diagnostics, aka goodness-of-fit (GOF) diagnostics

This page demonstrates the use of bbr.bayes, and other tools, to generate MCMC diagnostics for NONMEM® Bayesian (Bayes) models.

There is no explicit functionality in bbr.bayes to perform these steps; however, the output from bbr.bayes makes these steps relatively simple.

Tools used

MetrumRG packages

bbr Manage, track, and report modeling activities, through simple R objects, with a user-friendly interface between R and NONMEM®.

bbr.bayes Extension of the bbr package to support Bayesian modeling with Stan or NONMEM®.

CRAN packages

dplyr A grammar of data manipulation.

bayesplot Plotting Bayesian models and diagnostics with ggplot.

posterior Provides tools for working with output from Bayesian models, including output from CmdStan.

Set up

Load required packages and set file paths to your model and figure directories.

library(bbr)
library(bbr.bayes)
library(dplyr)
library(here)
library(tidyverse)
library(yspec)
library(posterior)
library(bayesplot)

MODEL_DIR <- here("model", "pk")

bayesplot::color_scheme_set('viridis')
theme_set(theme_bw())

MCMC diagnostics

After fitting the model, we examine a suite of MCMC diagnostics to see if anything is amiss with the sampling. We’ll focus on split R-hat, bulk and tail ESS, trace plots, and density plots. If any of these raise a flag about convergence, then additional diagnostics would be examined.

Model summary

We begin by reading in the output from our first base model, run 1000. This is done using the read_fit_model function from bbr.bayes, which returns a draws_array object from the posterior package.

model_name <- 1000
draws <- read_fit_model(file.path(MODEL_DIR, model_name))
n_chains <- nchains(draws)
n_iter <- niterations(draws)

draws_param <- subset_draws(draws, variable = c("THETA", "OMEGA", "SIGMA"))
draws_sum <- draws_param %>%  summarize_draws()

fixed <- is.na(draws_sum$rhat)
pars <- variables(draws_param)[!fixed]
draws_sum %>% 
  filter(variable %in% pars) %>% 
  mutate(across(-variable, ~ pmtables::sig(.x, maxex = 4)))
. # A tibble: 12 × 10
.    variable   mean   median sd      mad     q5     q95   rhat  ess_bulk ess_tail
.    <chr>      <chr>  <chr>  <chr>   <chr>   <chr>  <chr> <chr> <chr>    <chr>   
.  1 THETA[1]   0.475  0.475  0.0646  0.0625  0.369  0.581 1.00  309      841     
.  2 THETA[2]   4.10   4.10   0.0290  0.0285  4.05   4.15  1.00  1220     2330    
.  3 THETA[3]   1.10   1.10   0.0337  0.0319  1.05   1.16  0.999 3050     3460    
.  4 THETA[4]   4.23   4.23   0.0249  0.0246  4.19   4.27  1.00  422      712     
.  5 THETA[5]   1.30   1.30   0.0368  0.0375  1.24   1.36  1.00  180      459     
.  6 OMEGA[1,1] 0.257  0.251  0.0595  0.0564  0.171  0.366 1.01  363      771     
.  7 OMEGA[2,1] 0.0774 0.0758 0.0224  0.0219  0.0440 0.117 1.01  614      1450    
.  8 OMEGA[2,2] 0.0903 0.0894 0.0127  0.0125  0.0714 0.112 1.01  1460     2510    
.  9 OMEGA[3,1] 0.138  0.137  0.0277  0.0279  0.0962 0.186 1.00  1030     2260    
. 10 OMEGA[3,2] 0.0747 0.0739 0.0133  0.0131  0.0542 0.09… 1.00  1950     2320    
. 11 OMEGA[3,3] 0.176  0.175  0.0203  0.0201  0.144  0.210 0.999 3240     3700    
. 12 SIGMA[1,1] 0.0394 0.0394 0.00111 0.00115 0.0376 0.04… 1.00  2790     3530

For the population-level parameters, the R-hat values are all below 1.01. But, some ESS bulk and tail values are on the low side, particularly for THETA5 (intercompartmental clearance, Q).

R-hat plot

We can visualize the R-hat values with the mcmc_rhat function from bayesplot.

rhats <- draws_sum$rhat
names(rhats) <- draws_sum$variable
rhat_plot <- mcmc_rhat(rhats, pars = pars) + yaxis_text()
rhat_plot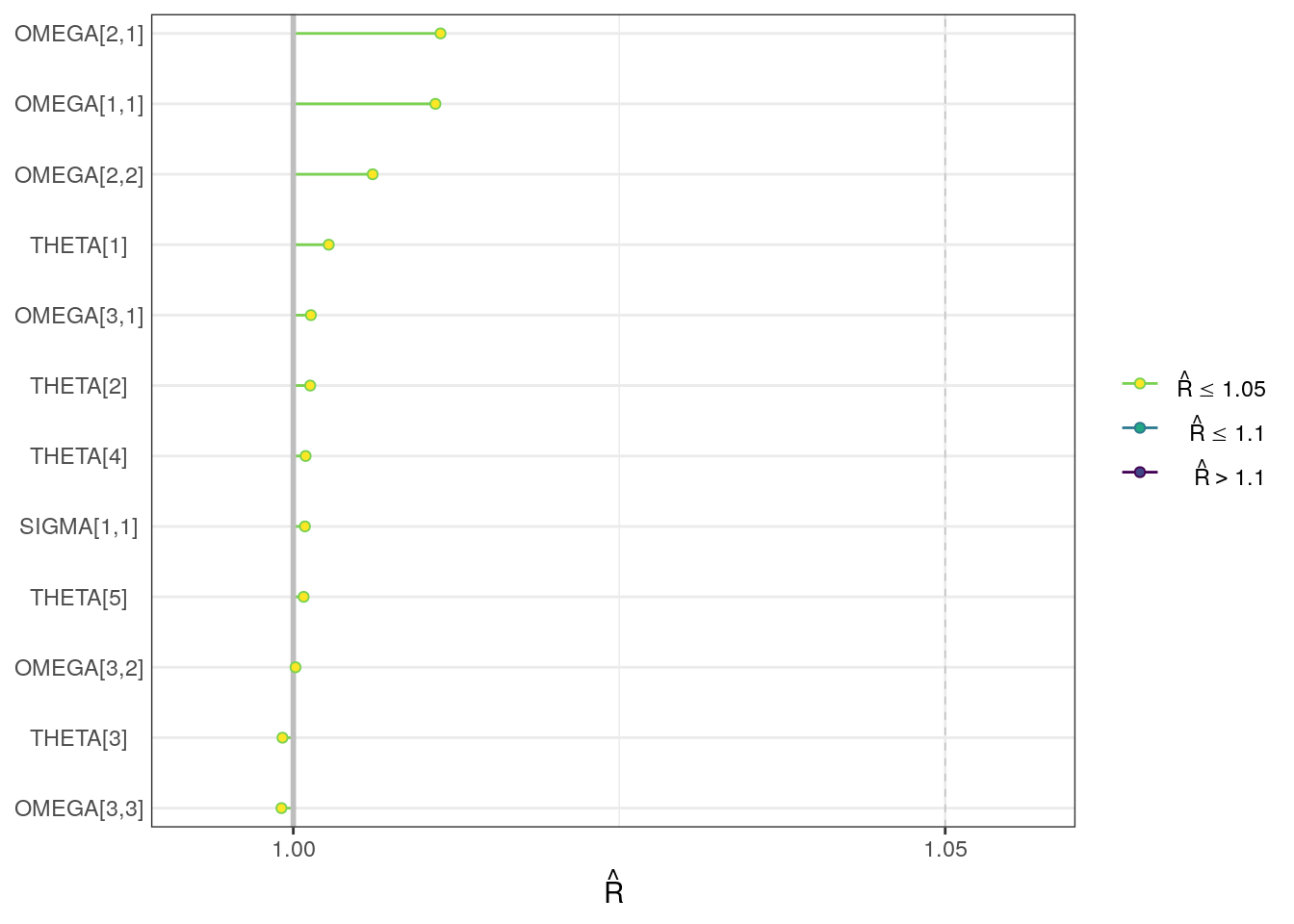

Figure 1: R-hat plot for model 1000.

ESS plots

We can also visualize the bulk and tail ESS as ratios of the effective sample size (Neff) to the total number of iterations (N). Further ESS plots are included in template-mcmc.Rmd.

ess_bulk <- draws_sum$ess_bulk
names(ess_bulk) <- draws_sum$variable
ess_bulk_ratios <- ess_bulk / (n_iter * n_chains)
ess_bulk_plot <- mcmc_neff(ess_bulk_ratios) + yaxis_text() +
  labs(title = "Bulk ESS ratios")
ess_bulk_plot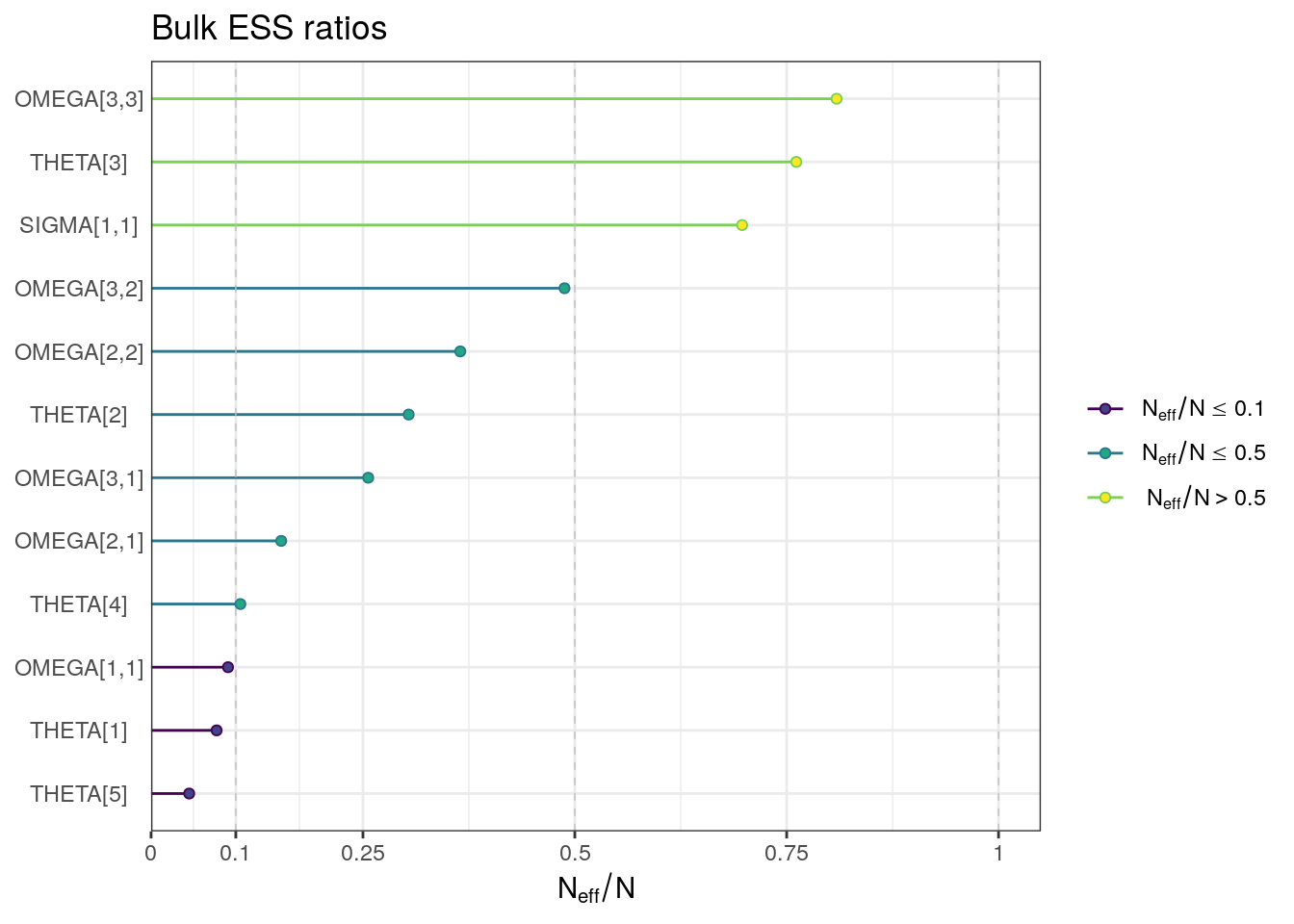

Figure 2: ESS bulk plot for model 1000.

ess_tail <- draws_sum$ess_tail
names(ess_tail) <- draws_sum$variable
ess_tail_ratios <- ess_tail / (n_iter * n_chains)
ess_tail_plot <- mcmc_neff(ess_tail_ratios) + yaxis_text() +
  labs(title = "Tail ESS ratios")
ess_tail_plot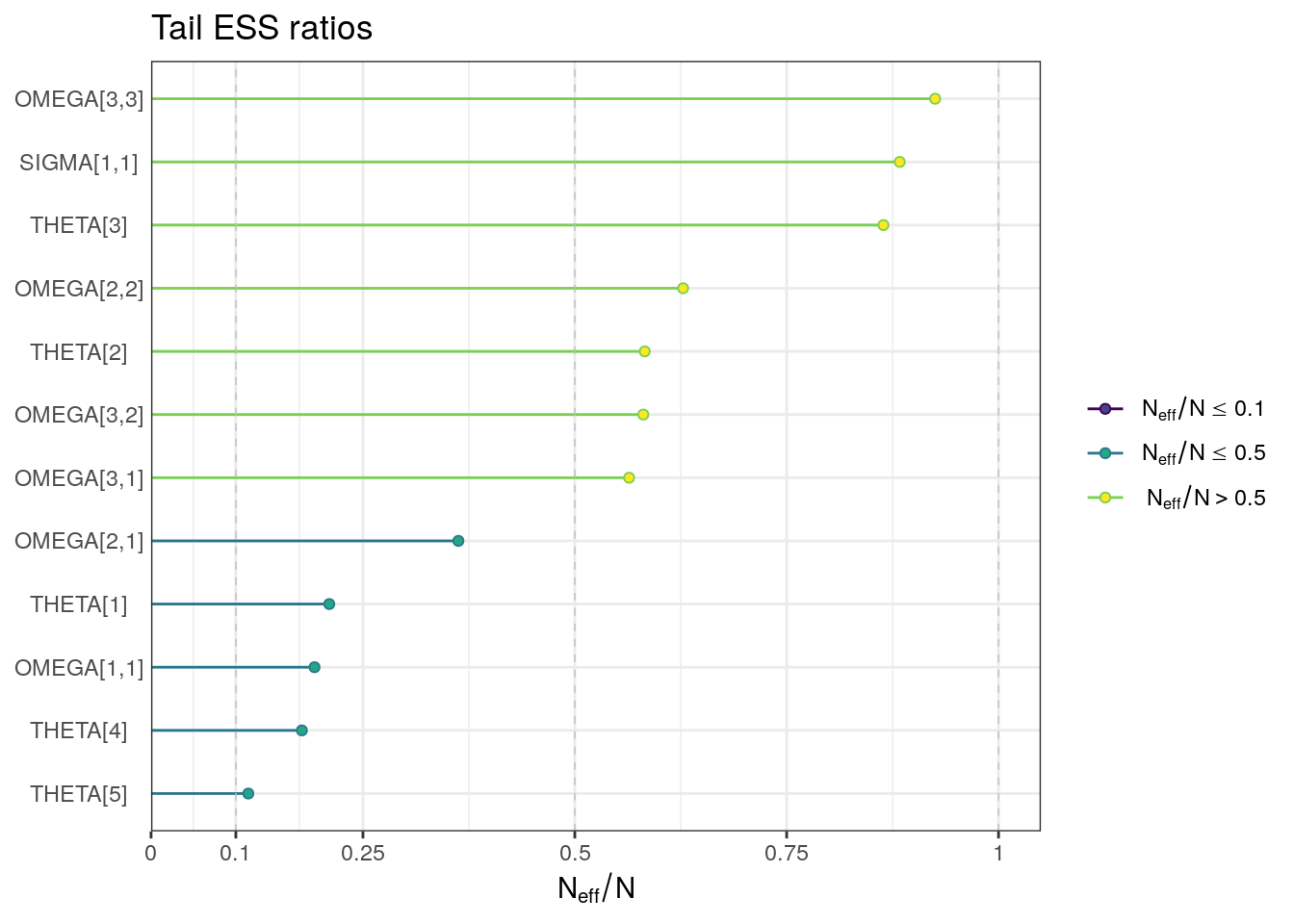

Figure 3: ESS tail plot for model 1000.

Trace and density plots

Next, we look at the trace and density plots.

trace0 <- mcmc_trace(draws, pars = pars)
trace0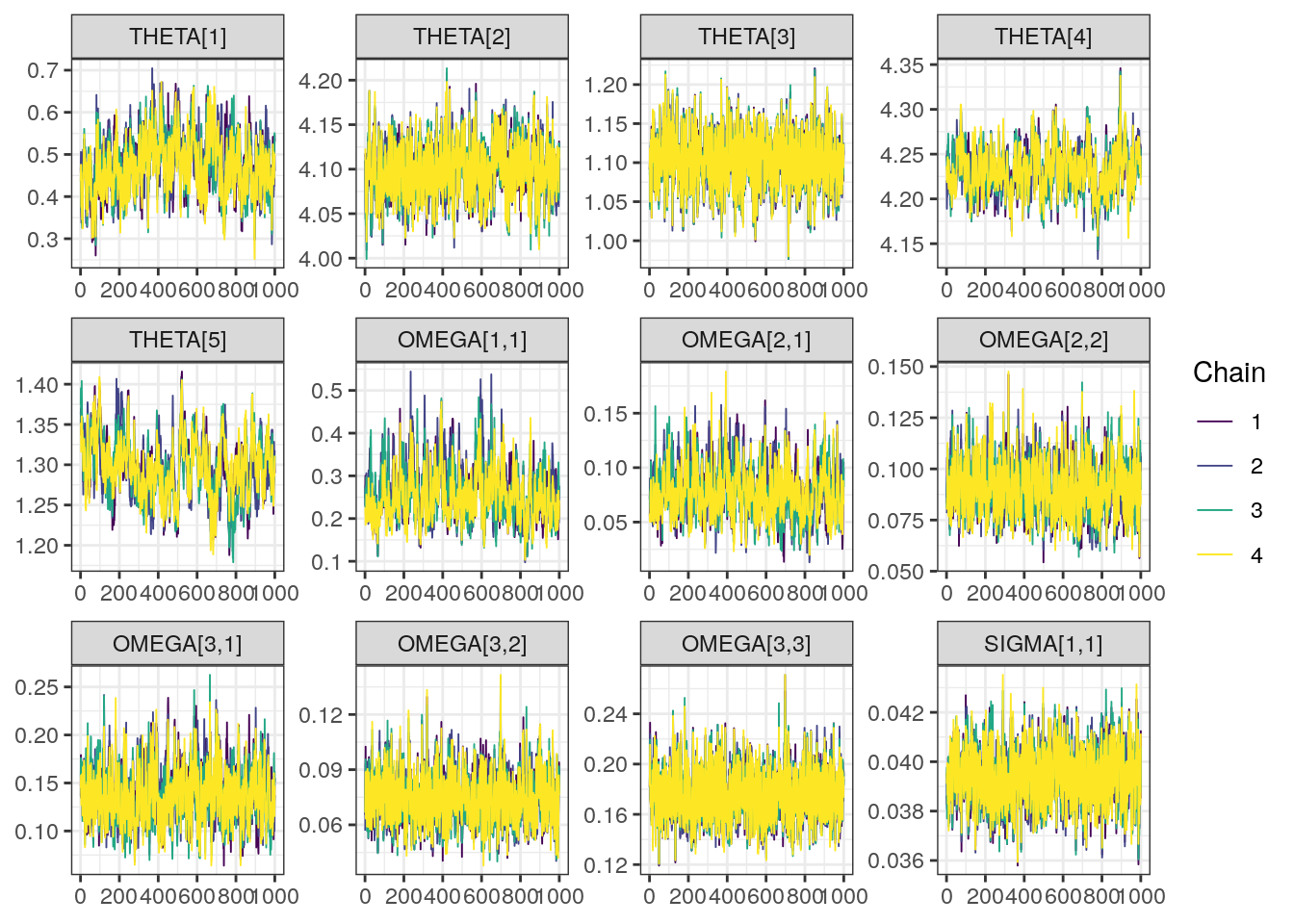

Figure 4: MCMC trace plots for model 1000.

density0 <- mcmc_dens_overlay(draws, pars = pars)
density0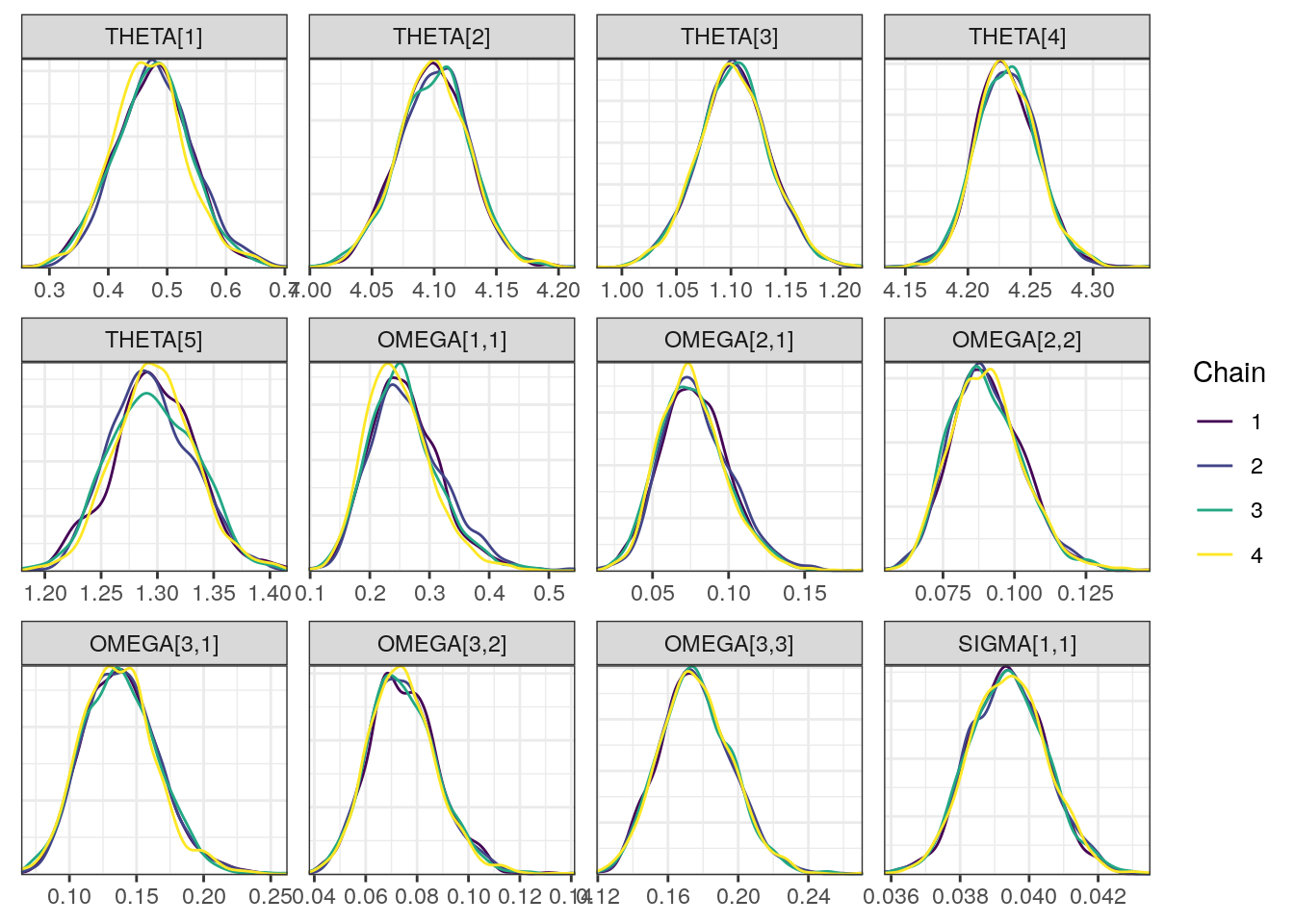

Figure 5: MCMC density plots for model 1000.

A scatterplot of the MCMC draws can be useful in showing bivariate relationships in the posterior distribution. The default scatterplot generated with mcmc_pairs uses points for the off-diagonal panels and histograms along the diagonal. We restrict this plot to only the THETAs to keep the size manageable.

mcmc_pairs(draws, regex_pars = "THETA")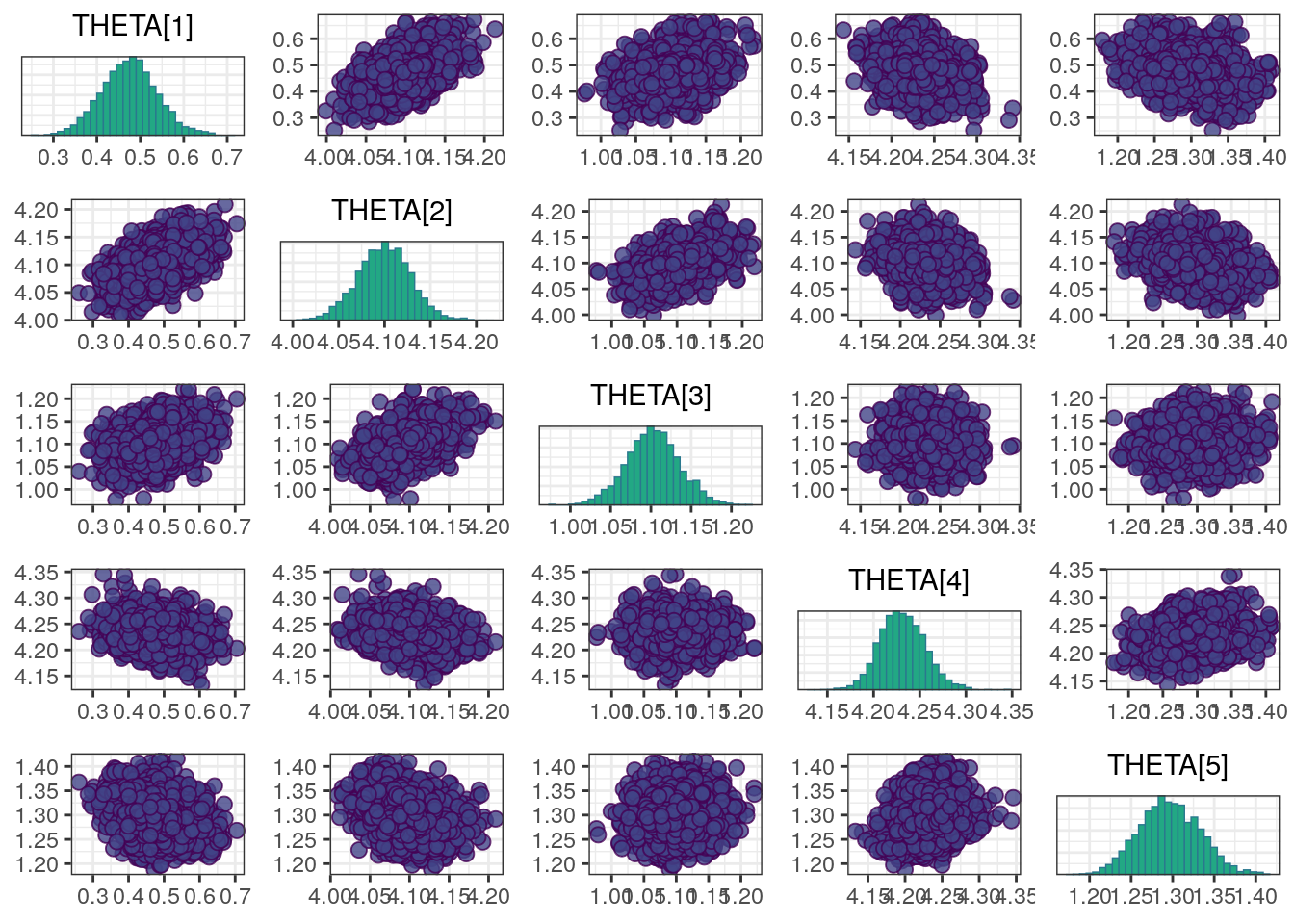

Although all R-hat values are low and scatterplots reasonable, some ESS values are on the low side which corresponds to some trace plots resembling “wiggly worms” than “fuzzy caterpillars.

Other resources

The following script from the GitHub repository is discussed on this page. If you’re interested running this code, visit the About the GitHub Repo page first.

MCMC Diagnostics template: template-mcmc.Rmd

More details on the visual MCMC diagnostics are available in a Vignettes from bayesplot package developers.