Update Model

Model revision workflow with bbr.bayes.

bbr
bbr.bayes
model management

Introduction

This page demonstrates an iterative, population pharmacokinetic (popPK) model development process using bbr and bbr.bayes consisting of a sequence of four models which includes ppkexpo1 implemented in the “Initial Model” section. While this is an oversimplification of a typical model development process, it is sufficient to illustrate key aspects of the use of the Metrum Reasearch Group (MetrumRG) Ecosystem (MERGE) tools for iterative model development.

All models share both the linear two compartment model with first order absorption and lognormal residual variation.

The sequence of four models is as follows:

  1. ppkexpo1
  • no individual-specific covariates
  • centered random effect parameterization
  1. ppkexpo2
  • no individual-specific covariates
  • non-centered random effect parameterization
  1. ppkexpo3
  • allometric scaling with fixed exponents on body weight
  • non-centered random effect parameterization
  1. ppkexpo4
  • allometric scaling with fixed exponents on body weight
  • additional covariates: eGFR, age, albumin
  • non-centered random effect parameterization

Tools used

MetrumRG packages

bbr Manage, track, and report modeling activities, through simple R objects, with a user-friendly interface between R and NONMEM®.

bbr.bayes Extension of the bbr package to support Bayesian modeling with Stan or NONMEM®.

CRAN packages

dplyr A grammar of data manipulation.

bayesplot Plotting Bayesian models and diagnostics with ggplot.

posterior Provides tools for working with output from Bayesian models, including output from CmdStan.

tidyvpc Create visual predictive checks using tidyverse-style syntax.

tidybayes Integrate Bayesian modeling with the tidyverse.

Set up

Load required packages and set file paths to your model and figure directories.

library(bbr)
library(bbr.bayes)
library(dplyr)
library(here)
library(tidyverse)
library(yspec)
library(cmdstanr)
library(tidyvpc)
library(posterior)
library(bayesplot)
library(tidybayes)
library(tidyvpc)
library(loo)
library(glue)
library(kableExtra)

set_cmdstan_path(path = here("Torsten", "v0.91.0", "cmdstan"))

MODEL_DIR <- here("model", "stan")
FIGURE_DIR <- here("deliv", "figure")

## load tags}
TAGS <- yaml::read_yaml(here("script", "tags.yaml"))

Model creation and submission

Read in the base model (ppkexpo1). We will revise it to generate our revised model.

ppkexpo1 <- read_model(here(MODEL_DIR, "ppkexpo1"))

Revised model—non-centered parameterization

ppkexpo1 provided a small divergent transition value. Let’s try improving sampling performance by changing from a centered parameterization to a non-centered one. Copy ppkexpo1 and revise it.

ppkexpo2 <- copy_model_from(ppkexpo1, "ppkexpo2", .inherit_tags = TRUE, 
                      .overwrite = TRUE) %>%
  replace_tag(TAGS$CP, TAGS$NCP) %>%
  add_description("Base popPK model with non-centered parameterization")

Now, manually edit ppkexpo2.stan and ppkexpo2-init.R to implement a non-centered parameterization. For this demo, copy the previously created files from the demo folder.

ppkexpo2 <- ppkexpo2 %>%
  add_stanmod_file(here(MODEL_DIR, "demo", "ppkexpo2.stan")) %>%
  add_staninit_file(here(MODEL_DIR, "demo", "ppkexpo2-init.R"))

Here is the revised Stan model implementing the two compartmental popPK model with a non-centered parameterization. With this parameterization, the individual PK parameters are not sampled directly from a multivariate normal distribution. Instead, standard normal, random variables are sampled; and the multivariate normal, PK parameters are constructed using some matrix algebra, including the Cholesky decomposition of the correlation matrix.

. /*
. Base PPK model
.   - Linear 2 compartment
.   - Non-centered parameterization
.   - lognormal residual variation
.   
. Based on NONMEM PopPK FOCE example project
. */
. 
. data{
.   int<lower = 1> nId; // number of individuals
.   int<lower = 1> nt; // number of events (rows in data set)
.   int<lower = 1> nObs; // number of PK observations
.   array[nObs] int<lower = 1> iObs; // event indices for PK observations
.   int<lower = 1> nBlq; // number of BLQ observations
.   array[nBlq] int<lower = 1> iBlq; // event indices for BLQ observations
.   array[nt] real<lower = 0> amt, time;
.   array[nt] int<lower = 1> cmt;
.   array[nt] int<lower = 0> evid;
.   array[nId] int<lower = 1> start, end; // indices of first & last observations
.   vector<lower = 0>[nObs] cObs;
.   real<lower = 0> LOQ;
. }
. 
. transformed data{
.   int<lower = 1> nRandom = 5, nCmt = 3;
.   array[nt] real<lower = 0> rate = rep_array(0.0, nt), 
.                             ii = rep_array(0.0, nt);
.   array[nt] int<lower = 0> addl = rep_array(0, nt), 
.                            ss = rep_array(0, nt);
.   array[nId, nCmt] real F = rep_array(1.0, nId, nCmt), 
.                         tLag = rep_array(0.0, nId, nCmt);
.   }
. 
. parameters{
.   real<lower = 0> CLHat, QHat, V2Hat, V3Hat;
. // To constrain kaHat > lambda1 uncomment the following
.   real<lower = (CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat +
.       sqrt((CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat)^2 -
.            4 * CLHat / V2Hat * QHat / V3Hat)) / 2> kaHat; // ka > lambda_1
.   
.   real<lower = 0> sigma;
.   vector<lower = 0>[nRandom] omega;
. //  corr_matrix[nRandom] rho;
. //  array[nId] vector[nRandom] theta;
.   cholesky_factor_corr[nRandom] L_corr;
.   matrix[nRandom, nId] z;
. }
. 
. transformed parameters{
.   vector[nRandom] thetaHat = log([CLHat, QHat, V2Hat, V3Hat, kaHat]');
.   // Individual parameters
.   matrix[nId, nRandom] theta = (rep_matrix(thetaHat, nId) + diag_pre_multiply(omega, L_corr * z))';
.   vector<lower = 0>[nId] CL = exp(theta[,1]),
.                          Q = exp(theta[,2]),
.                          V2 = exp(theta[,3]),
.                          V3 = exp(theta[,4]),
.                          ka = exp(theta[,5]);
.   corr_matrix[nRandom] rho =  L_corr * L_corr';
. 
.   row_vector[nt] cHat; // predicted concentration
.   matrix[nCmt, nt] x; // mass in all compartments
.   
.   for(j in 1:nId){
.     x[, start[j]:end[j]] = pmx_solve_twocpt(time[start[j]:end[j]],
.                                             amt[start[j]:end[j]],
.                                             rate[start[j]:end[j]],
.                                             ii[start[j]:end[j]],
.                                             evid[start[j]:end[j]],
.                                             cmt[start[j]:end[j]],
.                                             addl[start[j]:end[j]],
.                                             ss[start[j]:end[j]],
.                                             {CL[j], Q[j], V2[j], V3[j], ka[j]});
. 
.     cHat[start[j]:end[j]] = x[2, start[j]:end[j]] / V2[j];
.   }
. }
. 
. model{
.   // priors
.   CLHat ~ normal(0, 10); 
.   QHat ~ normal(0, 10);
.   V2Hat ~ normal(0, 50);
.   V3Hat ~ normal(0, 100);
.   kaHat ~ normal(0, 3);
.   sigma ~ normal(0, 0.5);
.   omega ~ normal(0, 0.5); 
.   L_corr ~ lkj_corr_cholesky(2);
.   
.   // interindividual variability
.   to_vector(z) ~ normal(0, 1);
. 
.   // likelihood
.   cObs ~ lognormal(log(cHat[iObs]), sigma); // observed data likelihood
.   target += lognormal_lcdf(LOQ | log(cHat[iBlq]), sigma); // BLQ data likelihood
. 
. }
. 
. generated quantities{
.   // Individual parameters for hypothetical new individuals
.   matrix[nRandom, nId] zNew;
.   matrix[nId, nRandom] thetaNew;
.   vector<lower = 0>[nId] CLNew, QNew, V2New, V3New, kaNew;
. 
.   row_vector[nt] cHatNew; // predicted concentration in new individuals
.   matrix[nCmt, nt] xNew; // mass in all compartments in new individuals
.   array[nt] real cPred, cPredNew;
. 
.   vector[nObs + nBlq] log_lik;
. 
.   // Simulations for posterior predictive checks
.   for(j in 1:nId){
.     zNew[,j] = to_vector(normal_rng(rep_vector(0, nRandom), 1));
.   }
.   thetaNew = (rep_matrix(thetaHat, nId) + diag_pre_multiply(omega, L_corr * zNew))';
.   CLNew = exp(thetaNew[,1]);
.   QNew = exp(thetaNew[,2]);
.   V2New = exp(thetaNew[,3]);
.   V3New = exp(thetaNew[,4]);
.   kaNew = exp(thetaNew[,5]);
.   
.   for(j in 1:nId){
.     xNew[, start[j]:end[j]] = pmx_solve_twocpt(time[start[j]:end[j]],
.                                                amt[start[j]:end[j]],
.                                                rate[start[j]:end[j]],
.                                                ii[start[j]:end[j]],
.                                                evid[start[j]:end[j]],
.                                                cmt[start[j]:end[j]],
.                                                addl[start[j]:end[j]],
.                                                ss[start[j]:end[j]],
.                                                {CLNew[j], QNew[j], V2New[j], 
.                                                V3New[j], kaNew[j]});
. 
.     cHatNew[start[j]:end[j]] = xNew[2, start[j]:end[j]] / V2New[j];
. 
.     
.     cPred[start[j]] = 0.0;
.     cPredNew[start[j]] = 0.0;
.     // new observations in existing individuals
.     cPred[(start[j] + 1):end[j]] = lognormal_rng(log(cHat[(start[j] + 1):end[j]]), 
.       sigma);
.     // new observations in new individuals
.     cPredNew[(start[j] + 1):end[j]] = lognormal_rng(log(cHatNew[(start[j] + 1):end[j]]), 
.       sigma); 
.   }
.   
.   // Calculate log-likelihood values to use for LOO CV
.   
.   // Observation-level log-likelihood
.   for(i in 1:nObs)
.     log_lik[i] = lognormal_lpdf(cObs[i] | log(cHat[iObs[i]]), sigma);
.   for(i in 1:nBlq)
.     log_lik[i + nObs] = lognormal_lcdf(LOQ | log(cHat[iBlq[i]]), sigma);
. 
. }

We can compare two model files using the model_diff command. By default, the current model is compared to the model which it is based on (in this case, ppkexpo1).

model_diff(ppkexpo2)
. < ppkexpo2                               > ppkexpo1                             
. @@ 2,5 @@                                @@ 2,5 @@                              
.   Base PPK model                           Base PPK model                       
.     - Linear 2 compartment                   - Linear 2 compartment             
. <   - Non-centered parameterization      >   - Centered parameterization        
.     - lognormal residual variation           - lognormal residual variation     
.                                                                                 
. @@ 42,8 @@                               @@ 42,6 @@                             
.     real<lower = 0> sigma;                   real<lower = 0> sigma;             
.     vector<lower = 0>[nRandom] omega;        vector<lower = 0>[nRandom] omega;  
. < //  corr_matrix[nRandom] rho;          >   corr_matrix[nRandom] rho;          
. < //  array[nId] vector[nRandom] theta;  >   array[nId] vector[nRandom] theta;  
. <   cholesky_factor_corr[nRandom] L_cor  ~                                      
. : r;                                     ~                                      
. <   matrix[nRandom, nId] z;              ~                                      
.   }                                        }                                    
.                                                                                 
. @@ 51,11 @@                              @@ 49,12 @@                            
.     vector[nRandom] thetaHat = log([CLH      vector[nRandom] thetaHat = log([CLH
.   at, QHat, V2Hat, V3Hat, kaHat]');        at, QHat, V2Hat, V3Hat, kaHat]');    
.     // Individual parameters                 // Individual parameters           
. <   matrix[nId, nRandom] theta = (rep_m  ~                                      
. : atrix(thetaHat, nId) + diag_pre_multi  ~                                      
. : ply(omega, L_corr * z))';              ~                                      
. <   vector<lower = 0>[nId] CL = exp(the  >   array[nId] real<lower = 0> CL = exp
. : ta[,1]),                               : (theta[,1]),                         
.                            Q = exp(thet                                 Q = exp(
.   a[,2]),                                  theta[,2]),                          
.                            V2 = exp(the                                 V2 = exp
.   ta[,3]),                                 (theta[,3]),                         
.                            V3 = exp(the                                 V3 = exp
.   ta[,4]),                                 (theta[,4]),                         
.                            ka = exp(the                                 ka = exp
.   ta[,5]);                                 (theta[,5]);                         
. ~                                        >                                      
. ~                                        >   // Covariance matrix               
. <   corr_matrix[nRandom] rho =  L_corr   >   cov_matrix[nRandom] Omega = quad_fo
. : * L_corr';                             : rm_diag(rho, omega);                 
.                                                                                 
.     row_vector[nt] cHat; // predicted c      row_vector[nt] cHat; // predicted c
.   oncentration                             oncentration                         
. @@ 86,8 @@                               @@ 85,8 @@                             
.     sigma ~ normal(0, 0.5);                  sigma ~ normal(0, 0.5);            
.     omega ~ normal(0, 0.5);                  omega ~ normal(0, 0.5);            
. <   L_corr ~ lkj_corr_cholesky(2);       >   rho ~ lkj_corr(2);                 
.                                                                                 
.     // interindividual variability           // interindividual variability     
. <   to_vector(z) ~ normal(0, 1);         >   theta ~ multi_normal(thetaHat, Omeg
. ~                                        : a);                                  
.                                                                                 
.     // likelihood                            // likelihood                      
. @@ 99,7 @@                               @@ 98,11 @@                            
.   generated quantities{                    generated quantities{                
.     // Individual parameters for hypoth      // Individual parameters for hypoth
.   etical new individuals                   etical new individuals               
. <   matrix[nRandom, nId] zNew;           >   array[nId] vector[nRandom] thetaNew
. ~                                        :  =                                   
. <   matrix[nId, nRandom] thetaNew;       >     multi_normal_rng(rep_array(thetaH
. ~                                        : at, nId), Omega);                    
. <   vector<lower = 0>[nId] CLNew, QNew,  >   array[nId] real<lower = 0> CLNew = 
. :  V2New, V3New, kaNew;                  : exp(thetaNew[,1]),                   
. ~                                        >                              QNew = e
. ~                                        : xp(thetaNew[,2]),                    
. ~                                        >                              V2New = 
. ~                                        : exp(thetaNew[,3]),                   
. ~                                        >                              V3New = 
. ~                                        : exp(thetaNew[,4]),                   
. ~                                        >                              kaNew = 
. ~                                        : exp(thetaNew[,5]);                   
.                                                                                 
.     row_vector[nt] cHatNew; // predicte      row_vector[nt] cHatNew; // predicte
.   d concentration in new individuals       d concentration in new individuals   
. @@ 110,14 @@                             @@ 113,4 @@                            
.                                                                                 
.     // Simulations for posterior predic      // Simulations for posterior predic
.   tive checks                              tive checks                          
. <   for(j in 1:nId){                     ~                                      
. <     zNew[,j] = to_vector(normal_rng(r  ~                                      
. : ep_vector(0, nRandom), 1));            ~                                      
. <   }                                    ~                                      
. <   thetaNew = (rep_matrix(thetaHat, nI  ~                                      
. : d) + diag_pre_multiply(omega, L_corr   ~                                      
. : * zNew))';                             ~                                      
. <   CLNew = exp(thetaNew[,1]);           ~                                      
. <   QNew = exp(thetaNew[,2]);            ~                                      
. <   V2New = exp(thetaNew[,3]);           ~                                      
. <   V3New = exp(thetaNew[,4]);           ~                                      
. <   kaNew = exp(thetaNew[,5]);           ~                                      
. <                                        ~                                      
.     for(j in 1:nId){                         for(j in 1:nId){                   
.       xNew[, start[j]:end[j]] = pmx_sol        xNew[, start[j]:end[j]] = pmx_sol
.   ve_twocpt(time[start[j]:end[j]],         ve_twocpt(time[start[j]:end[j]],     
. @@ 133,5 @@                              @@ 126,4 @@                            
.                                                                                 
.       cHatNew[start[j]:end[j]] = xNew[2        cHatNew[start[j]:end[j]] = xNew[2
.   , start[j]:end[j]] / V2New[j];           , start[j]:end[j]] / V2New[j];       
. <                                        ~                                      
.                                                                                 
.       cPred[start[j]] = 0.0;                   cPred[start[j]] = 0.0;

ppkexpo2: Submit the model

## Set cmdstanr arguments
ppkexpo2 <- ppkexpo2 %>%
  set_stanargs(list(iter_warmup = 500,
                    iter_sampling = 500,
                    thin = 1,
                    chains = 4,
                    parallel_chains = 4,
##                    refresh = 10,
                    seed = 1234,
                    save_warmup = FALSE),
               .clear = TRUE)

## Check that the necessary files are present
check_stan_model(ppkexpo2)

## Fit the model using Stan
ppkexpo2_fit <- ppkexpo2 %>% submit_model(.overwrite = TRUE)

ppkexpo2: Parameter summary and sampling diagnostics

model_name <- "ppkexpo2"
mod <- read_model(here(MODEL_DIR, model_name))
fit <- read_fit_model(mod)

fit$cmdstan_diagnose()
. Processing csv files: /data/expo4-torsten-poppk/model/stan/ppkexpo2/ppkexpo2-output/ppkexpo2-202409271610-1-8e4be5.csv, /data/expo4-torsten-poppk/model/stan/ppkexpo2/ppkexpo2-output/ppkexpo2-202409271610-2-8e4be5.csv, /data/expo4-torsten-poppk/model/stan/ppkexpo2/ppkexpo2-output/ppkexpo2-202409271610-3-8e4be5.csv, /data/expo4-torsten-poppk/model/stan/ppkexpo2/ppkexpo2-output/ppkexpo2-202409271610-4-8e4be5.csv
. 
. Checking sampler transitions treedepth.
. Treedepth satisfactory for all transitions.
. 
. Checking sampler transitions for divergences.
. No divergent transitions found.
. 
. Checking E-BFMI - sampler transitions HMC potential energy.
. E-BFMI satisfactory.
. 
. Effective sample size satisfactory.
. 
. The following parameters had split R-hat greater than 1.05:
.   CLHat, L_corr[3,2], L_corr[5,2], z[1,78], thetaHat[1]
. Such high values indicate incomplete mixing and biased estimation.
. You should consider regularizating your model with additional prior information or a more effective parameterization.
. 
. Processing complete.
pars <- c("lp__", "CLHat", "QHat", "V2Hat", "V3Hat", "kaHat",
          "sigma", glue("omega[{1:5}]"),
          paste0("rho[", matrix(apply(expand.grid(1:5, 1:5),
                                      1, paste, collapse = ","),
                                ncol = 5)[upper.tri(diag(5), 
                                                    diag = FALSE)], "]"))
# Get posterior samples for parameters of interest
posterior <- fit$draws(variables = pars)
# Get quantities related to NUTS performance, e.g., occurrence of
# divergent transitions
np <- nuts_params(fit) 

n_iter <- dim(posterior)[1]
n_chains <- dim(posterior)[2]

ptable <- fit$summary(variables = pars) %>%
  mutate(across(-variable, ~ pmtables::sig(.x, maxex = 4))) %>% 
  rename(parameter = variable) %>%
  mutate("90% CI" = paste("(", q5, ", ", q95, ")", 
                          sep = "")) %>%
  select(parameter, mean, median, sd, mad, "90% CI", ess_bulk, ess_tail, rhat)

ptable %>% 
  kable %>%
  kable_styling()
parameter mean median sd mad 90% CI ess_bulk ess_tail rhat
lp__ -32.9 -31.8 28.2 28.3 (-82.6, 12.1) 295 674 1.01
CLHat 3.14 3.14 0.114 0.111 (2.94, 3.32) 47.7 41.5 1.08
QHat 3.75 3.74 0.172 0.171 (3.47, 4.04) 578 1630 1.00
V2Hat 61.7 61.6 2.27 2.32 (57.9, 65.4) 174 383 1.03
V3Hat 67.6 67.5 1.90 1.89 (64.6, 70.8) 948 1500 1.00
kaHat 1.64 1.64 0.124 0.121 (1.45, 1.86) 453 906 1.01
sigma 0.214 0.214 0.00306 0.00315 (0.209, 0.219) 1790 1500 1.00
omega[1] 0.438 0.437 0.0253 0.0253 (0.397, 0.478) 84.5 207 1.05
omega[2] 0.119 0.118 0.0649 0.0707 (0.0188, 0.225) 249 346 1.01
omega[3] 0.378 0.377 0.0268 0.0267 (0.336, 0.424) 375 638 1.01
omega[4] 0.181 0.180 0.0299 0.0299 (0.133, 0.231) 701 1300 1.00
omega[5] 0.540 0.536 0.0726 0.0738 (0.425, 0.662) 509 1080 1.01
rho[1,2] -0.128 -0.141 0.278 0.283 (-0.565, 0.347) 2240 1270 1.00
rho[1,3] 0.671 0.674 0.0588 0.0585 (0.568, 0.764) 345 1070 1.02
rho[2,3] 0.0634 0.0590 0.267 0.274 (-0.362, 0.517) 139 447 1.02
rho[1,4] 0.339 0.344 0.138 0.135 (0.111, 0.555) 1570 1340 1.00
rho[2,4] 0.326 0.358 0.290 0.289 (-0.209, 0.757) 177 505 1.01
rho[3,4] 0.547 0.552 0.149 0.152 (0.281, 0.778) 584 996 1.00
rho[1,5] 0.607 0.609 0.0837 0.0859 (0.467, 0.743) 540 941 1.01
rho[2,5] -0.336 -0.386 0.322 0.317 (-0.778, 0.281) 103 260 1.04
rho[3,5] 0.431 0.433 0.103 0.104 (0.255, 0.596) 655 1100 1.00
rho[4,5] -0.0792 -0.0838 0.190 0.200 (-0.384, 0.227) 419 766 1.01

Trace and density plots

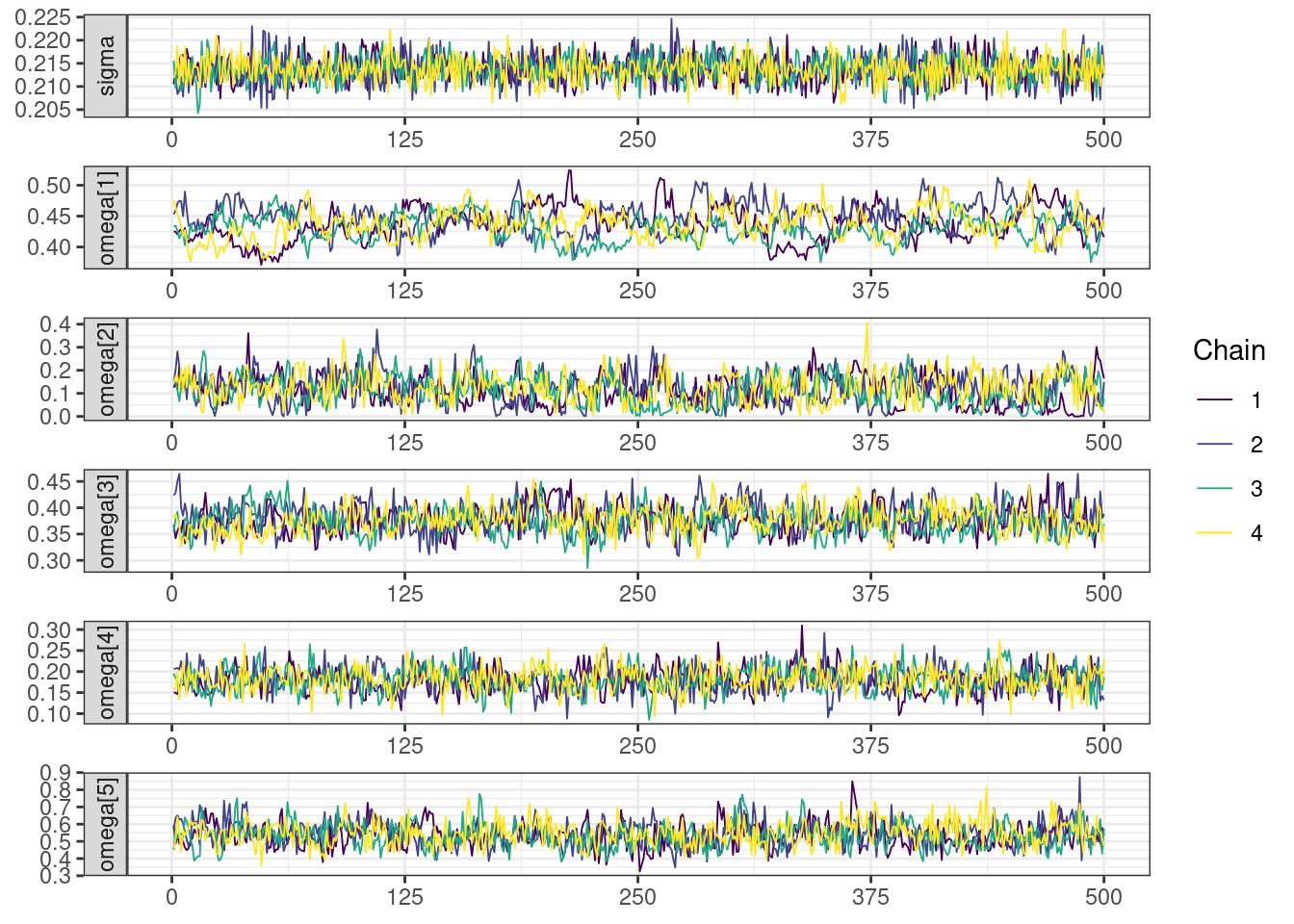
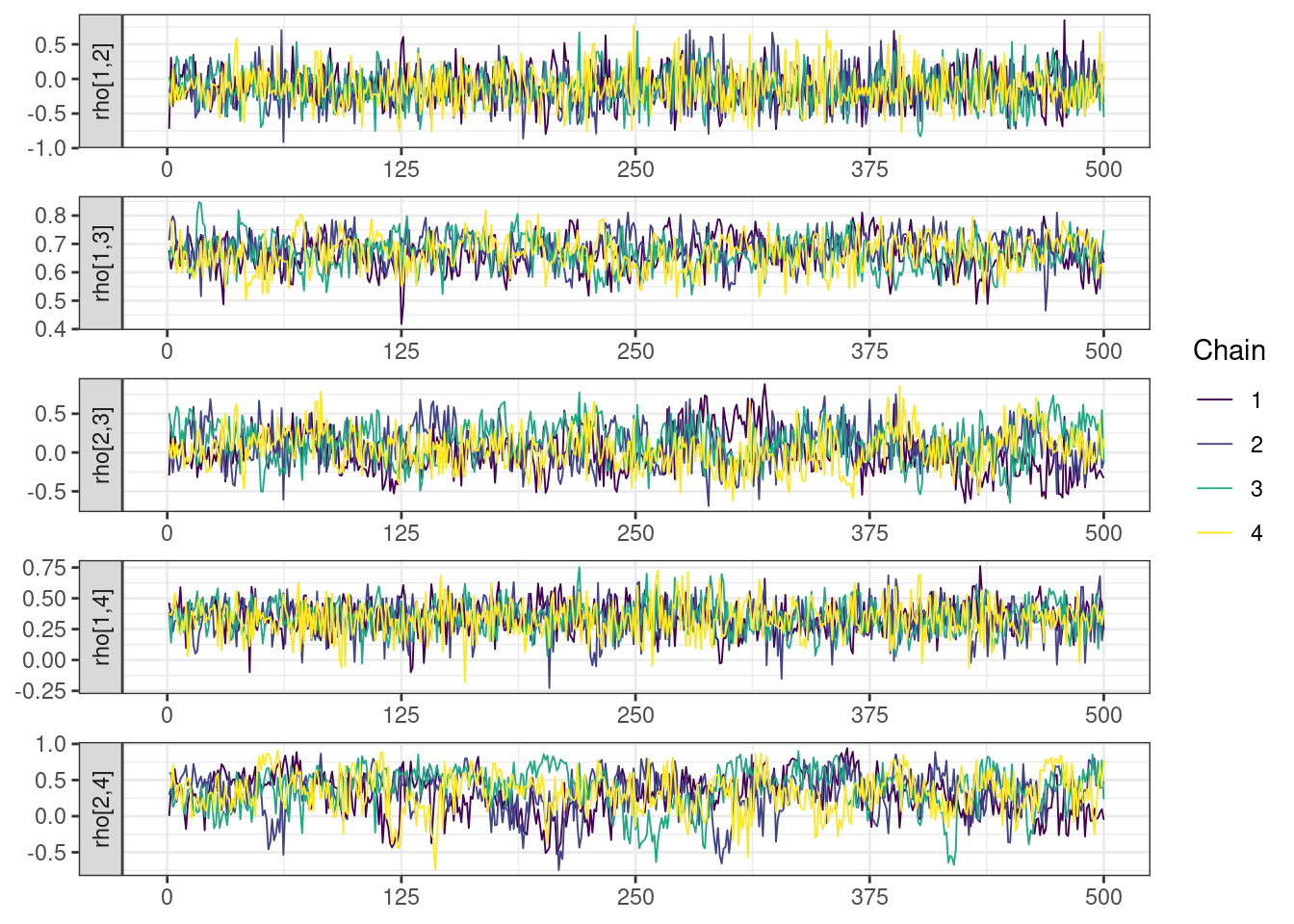
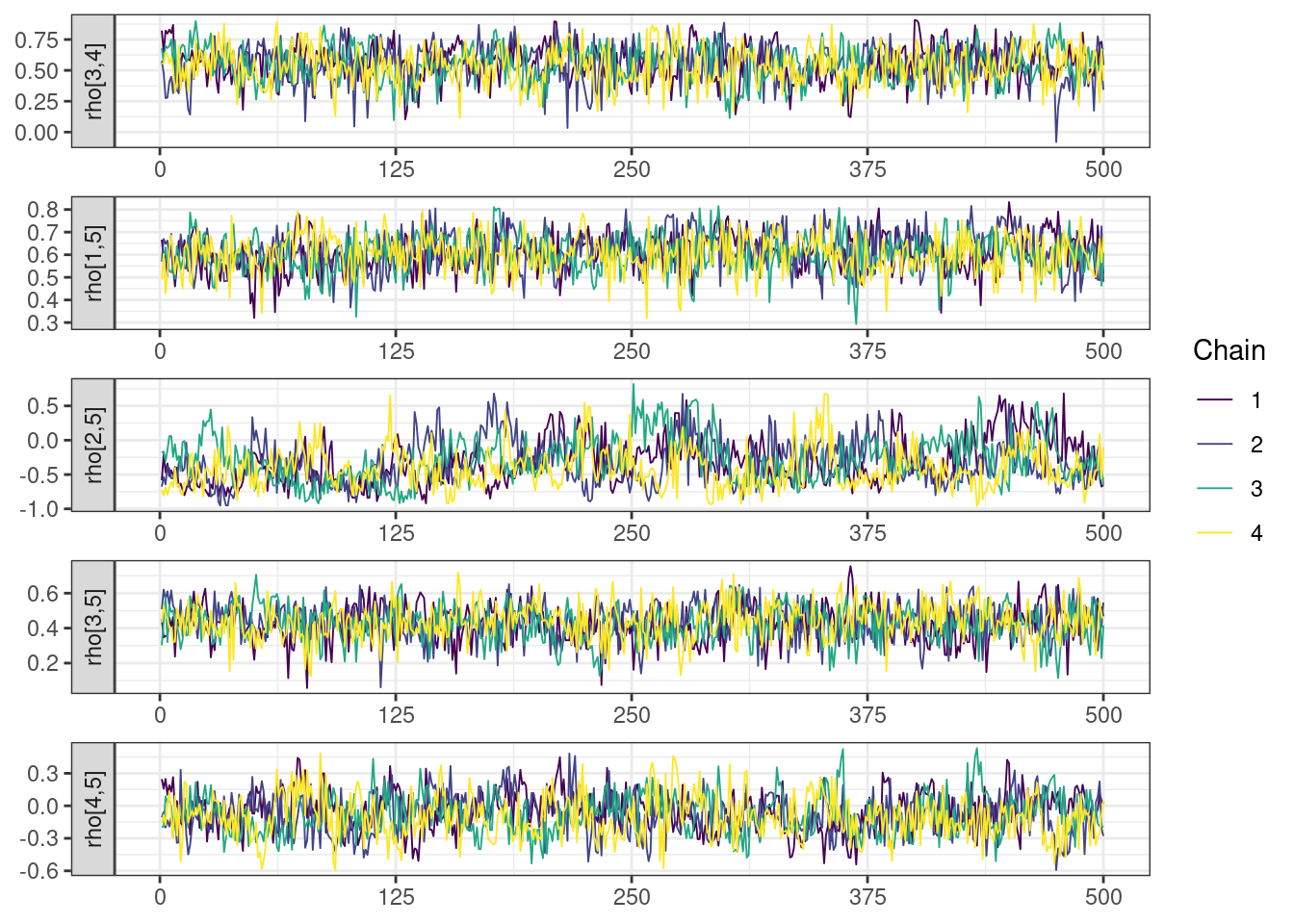
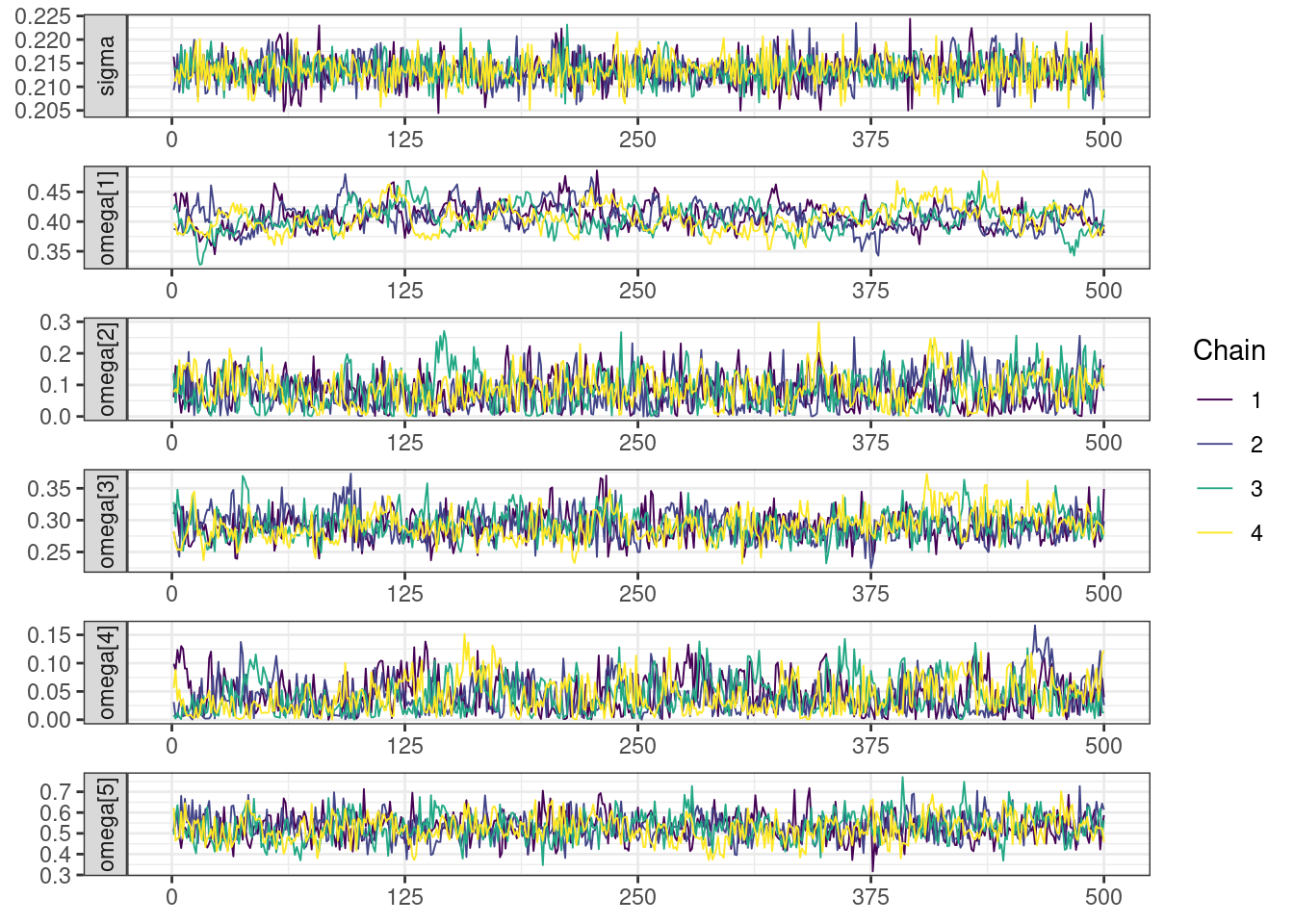
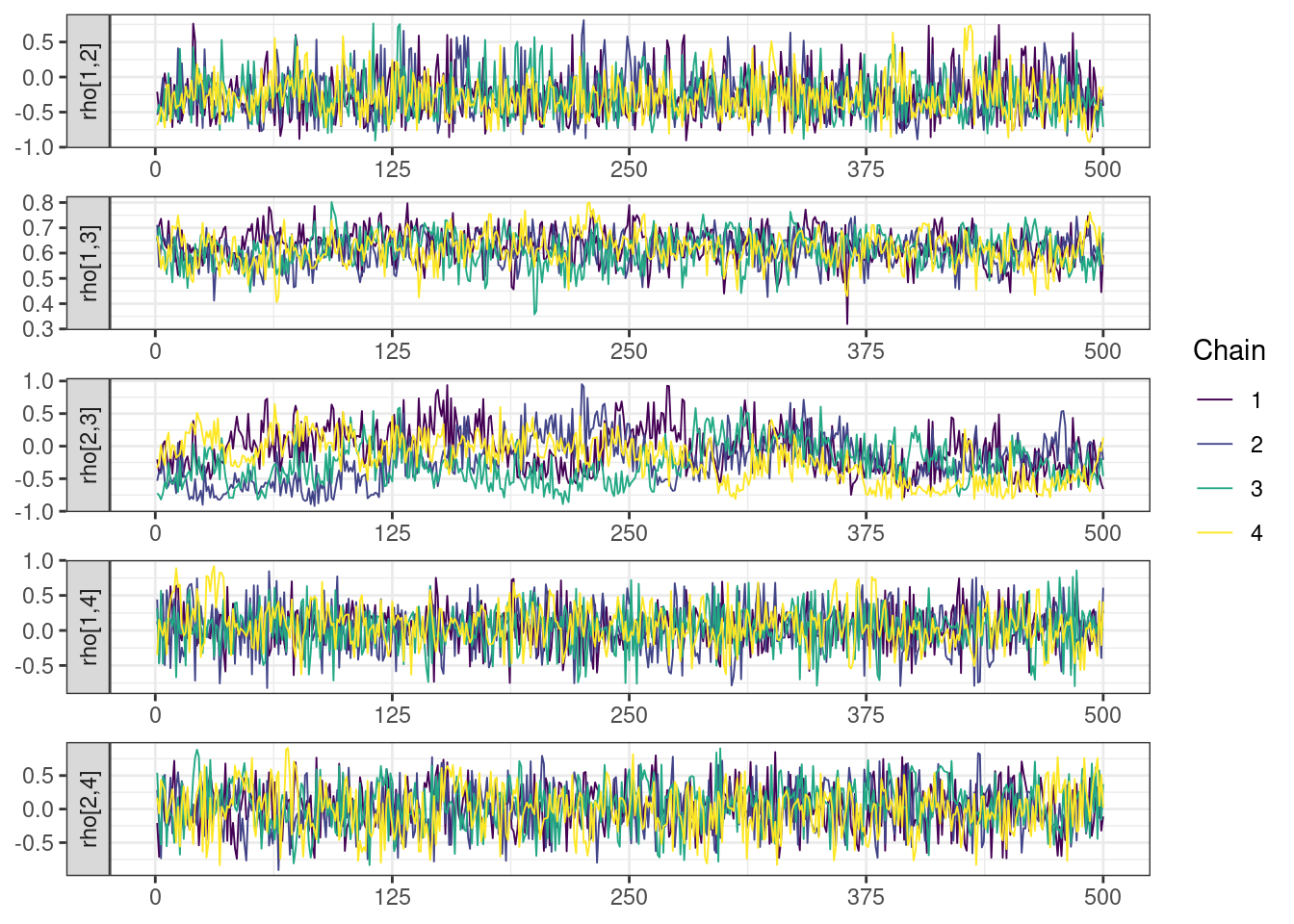
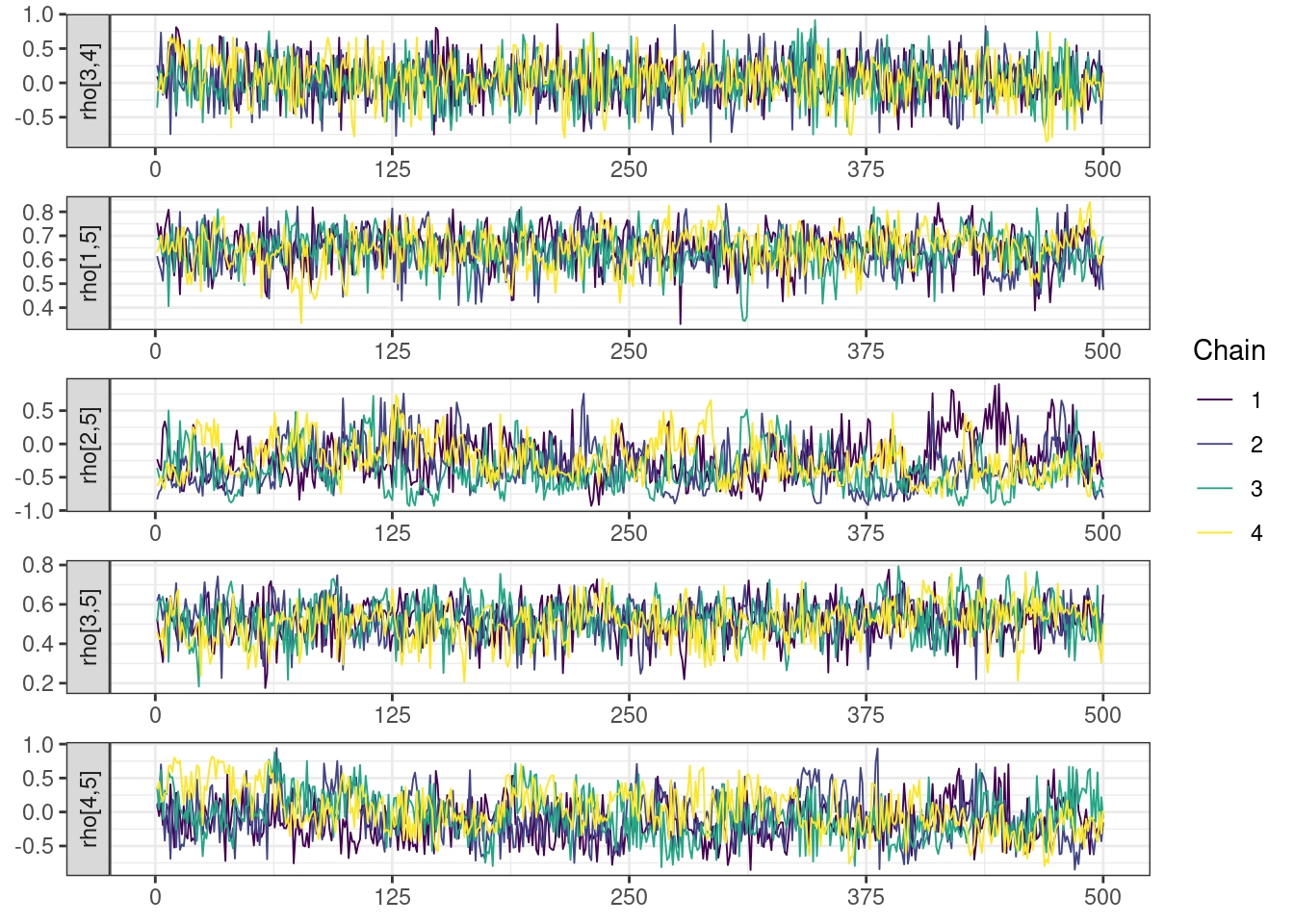
Next, we look at the trace and density plots.

mcmc_history_plots <- mcmc_history(posterior,
                                  nParPerPage = 6, 
                                  np = np)
mcmc_history_plots
. [[1]]
. 
. [[2]]
. 
. [[3]]
. 
. [[4]]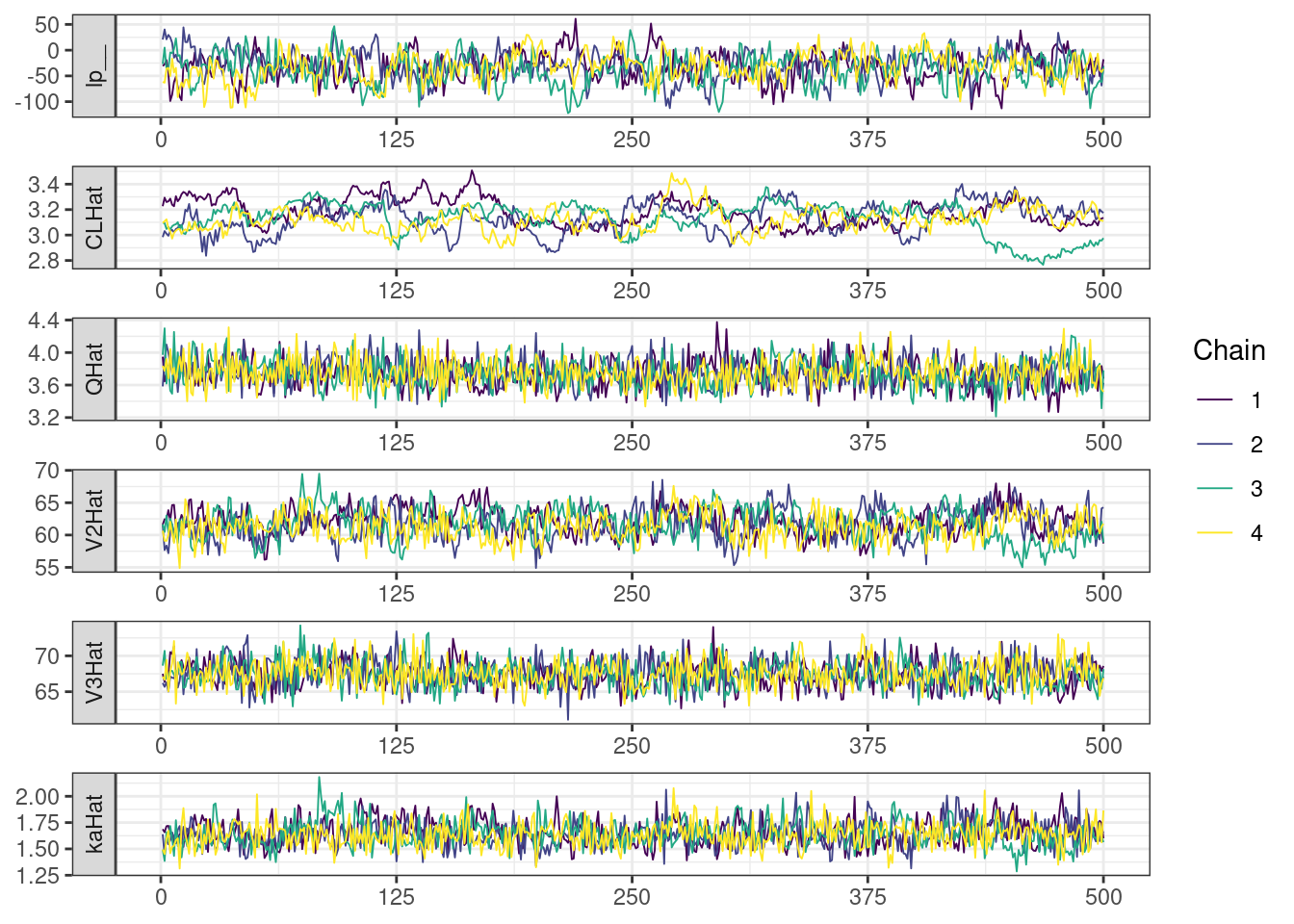

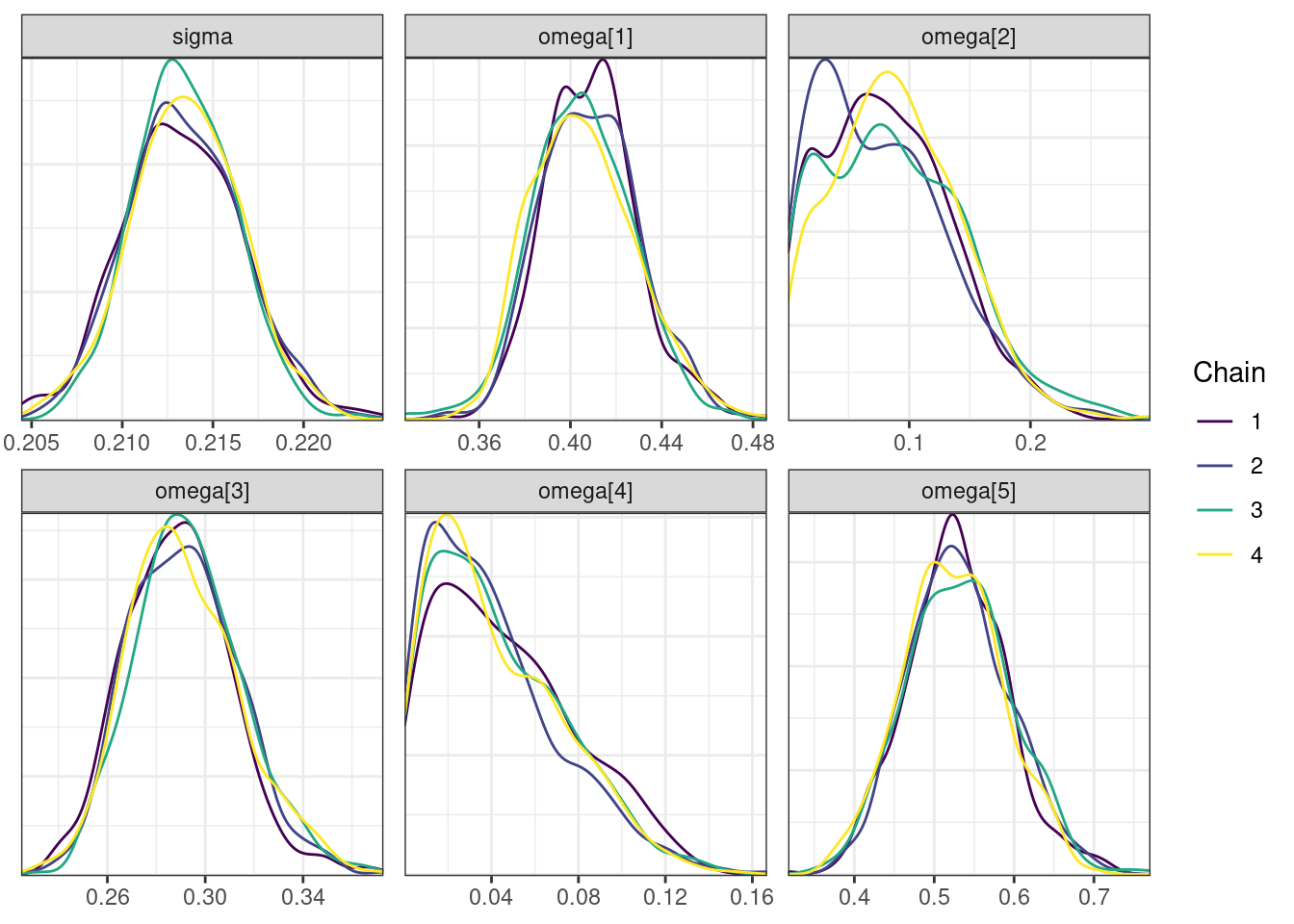
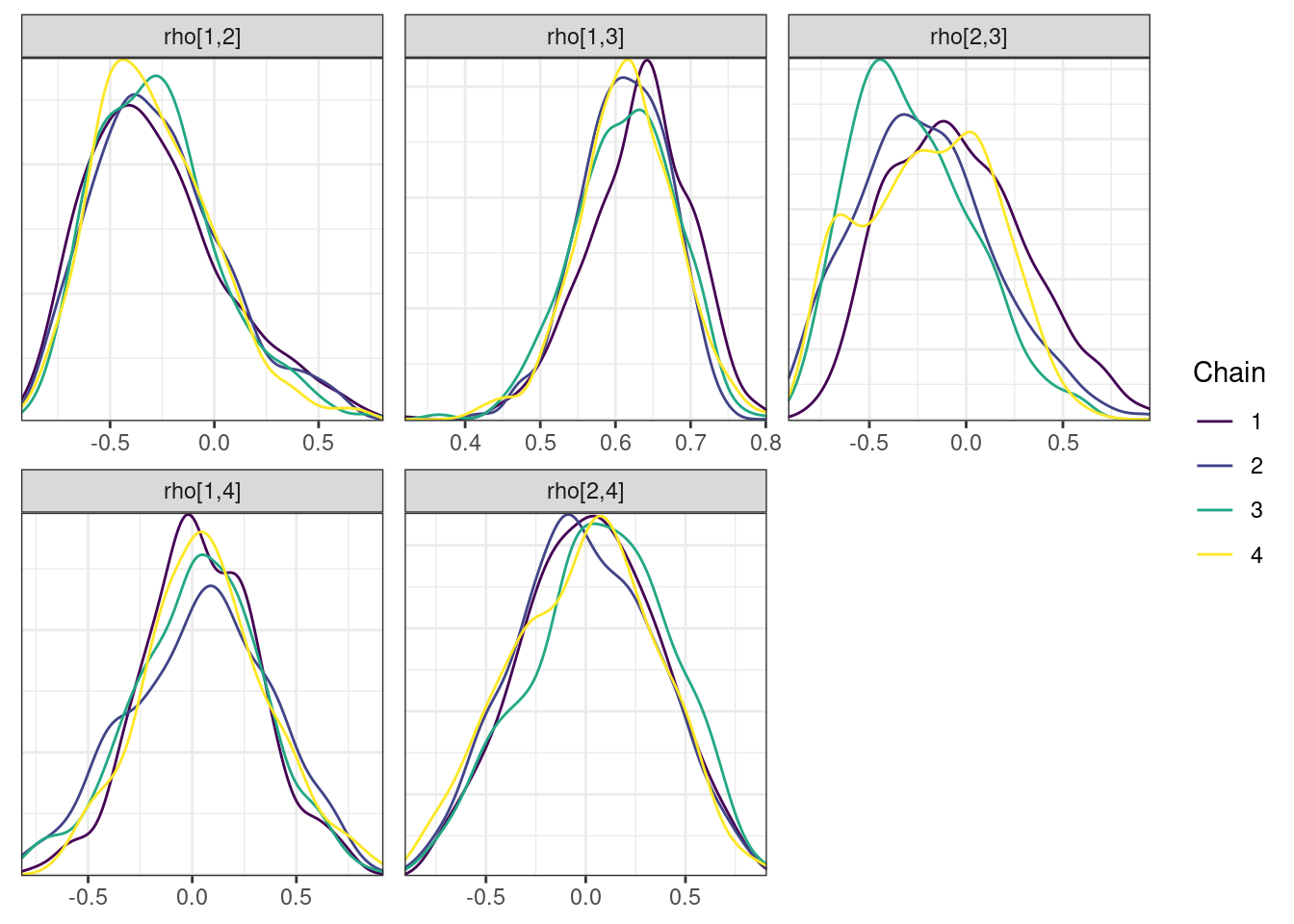
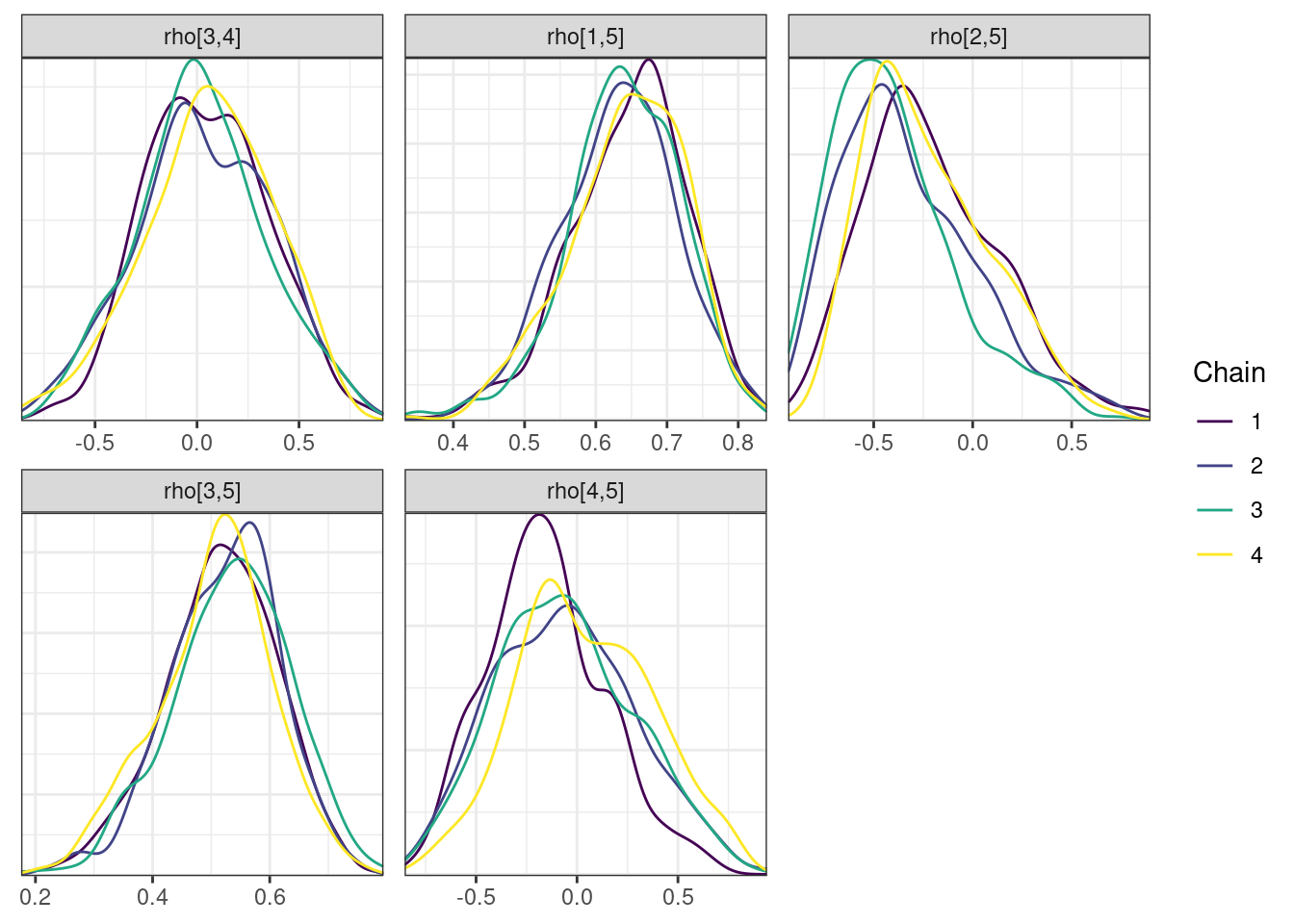
Figure 1: MCMC trace plots for model ppkexpo2.

Figure 2: MCMC trace plots for model ppkexpo2.

Figure 3: MCMC trace plots for model ppkexpo2.

Figure 4: MCMC trace plots for model ppkexpo2.
  mcmc_density_chain_plots <- mcmc_density(posterior, 
                                           nParPerPage = 6, byChain = TRUE)
mcmc_density_chain_plots
. [[1]]
. 
. [[2]]
. 
. [[3]]
. 
. [[4]]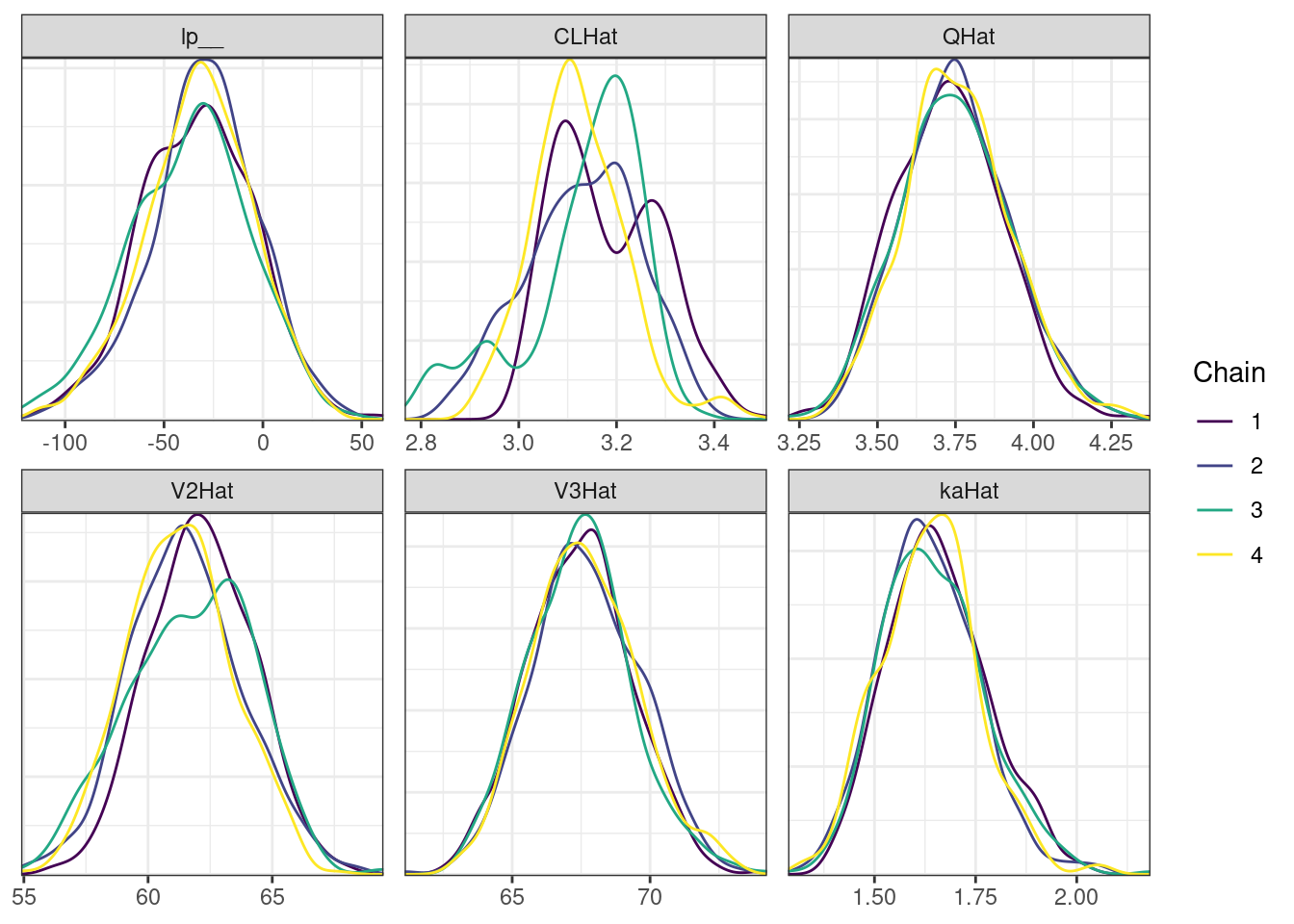

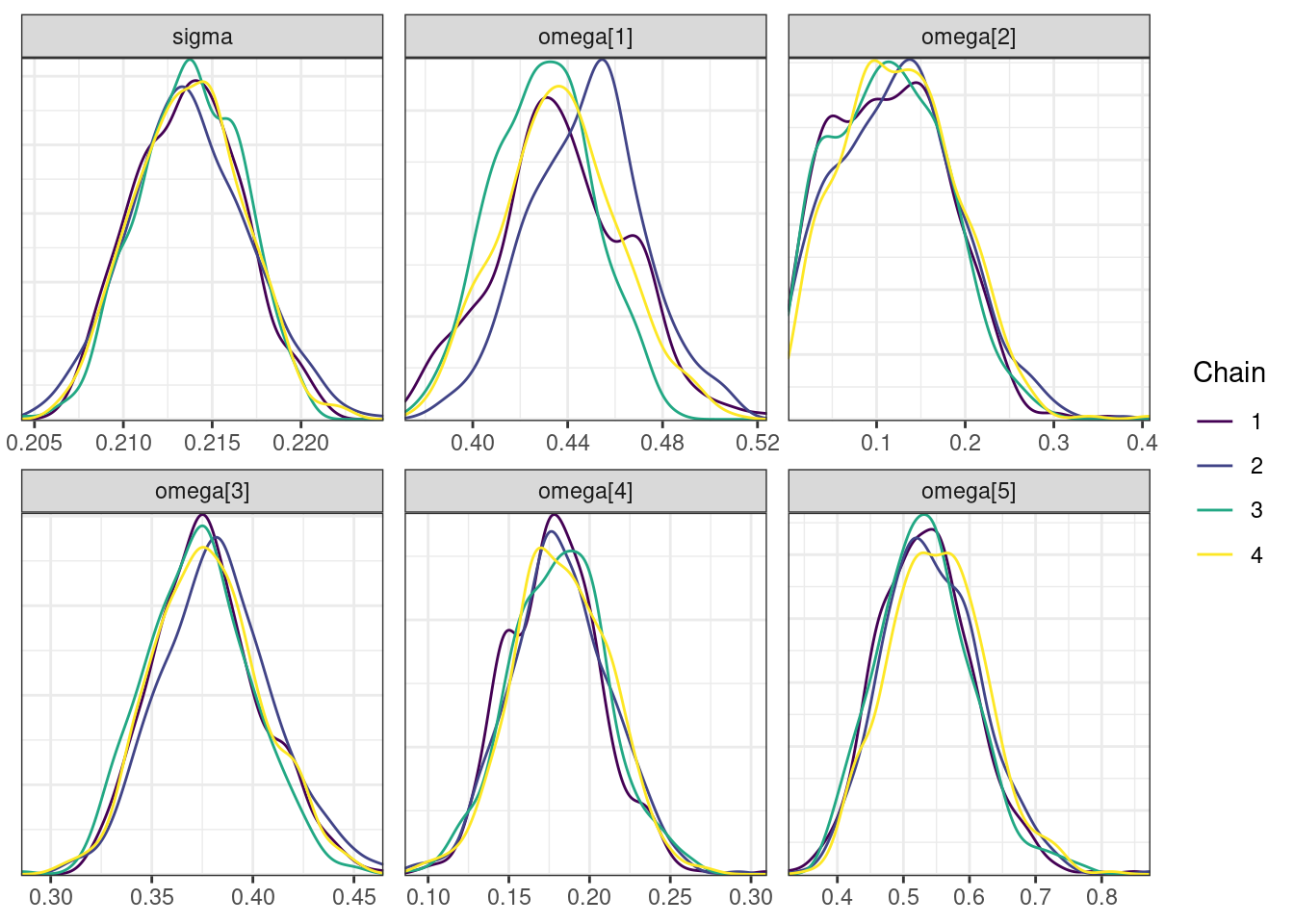
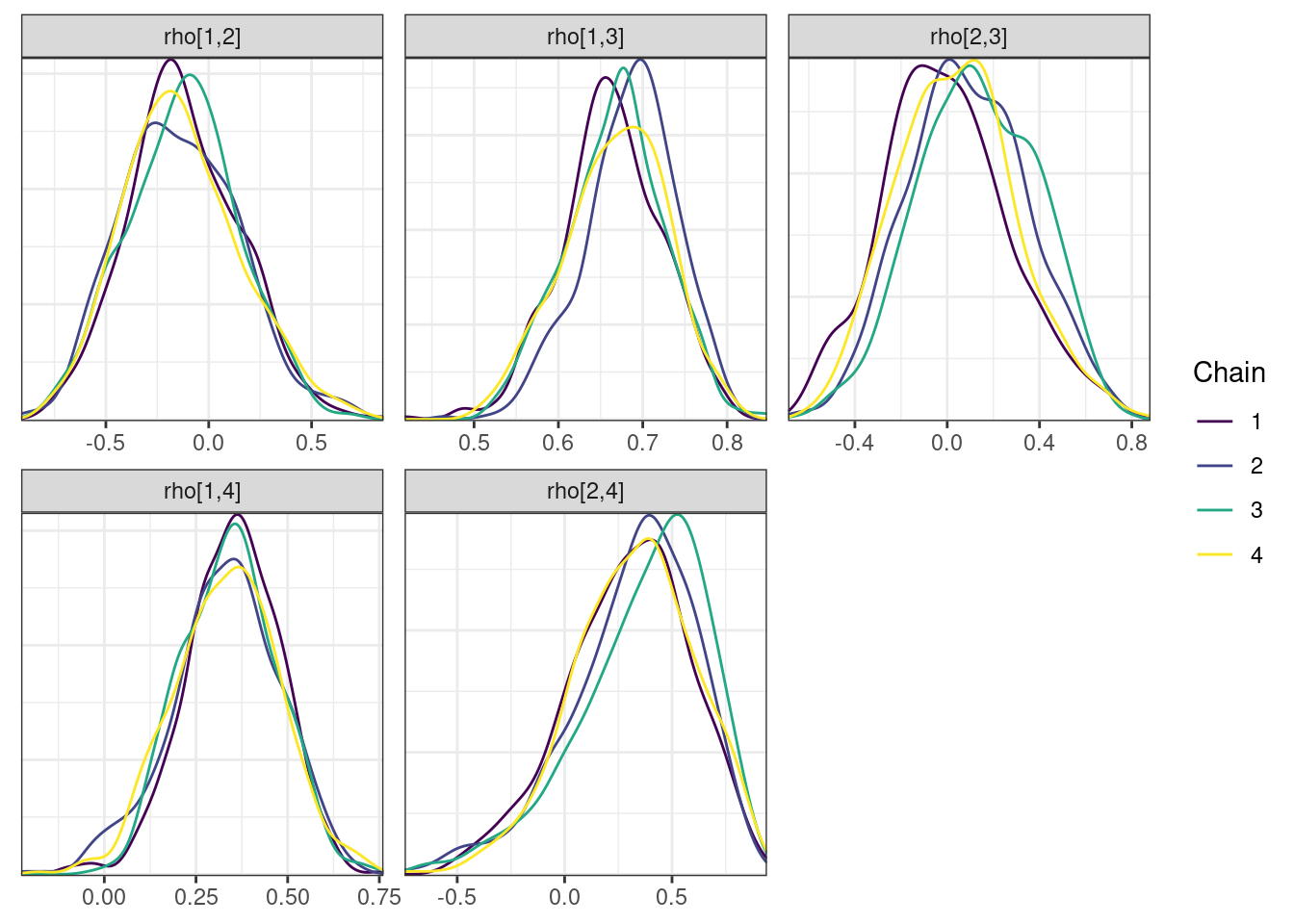
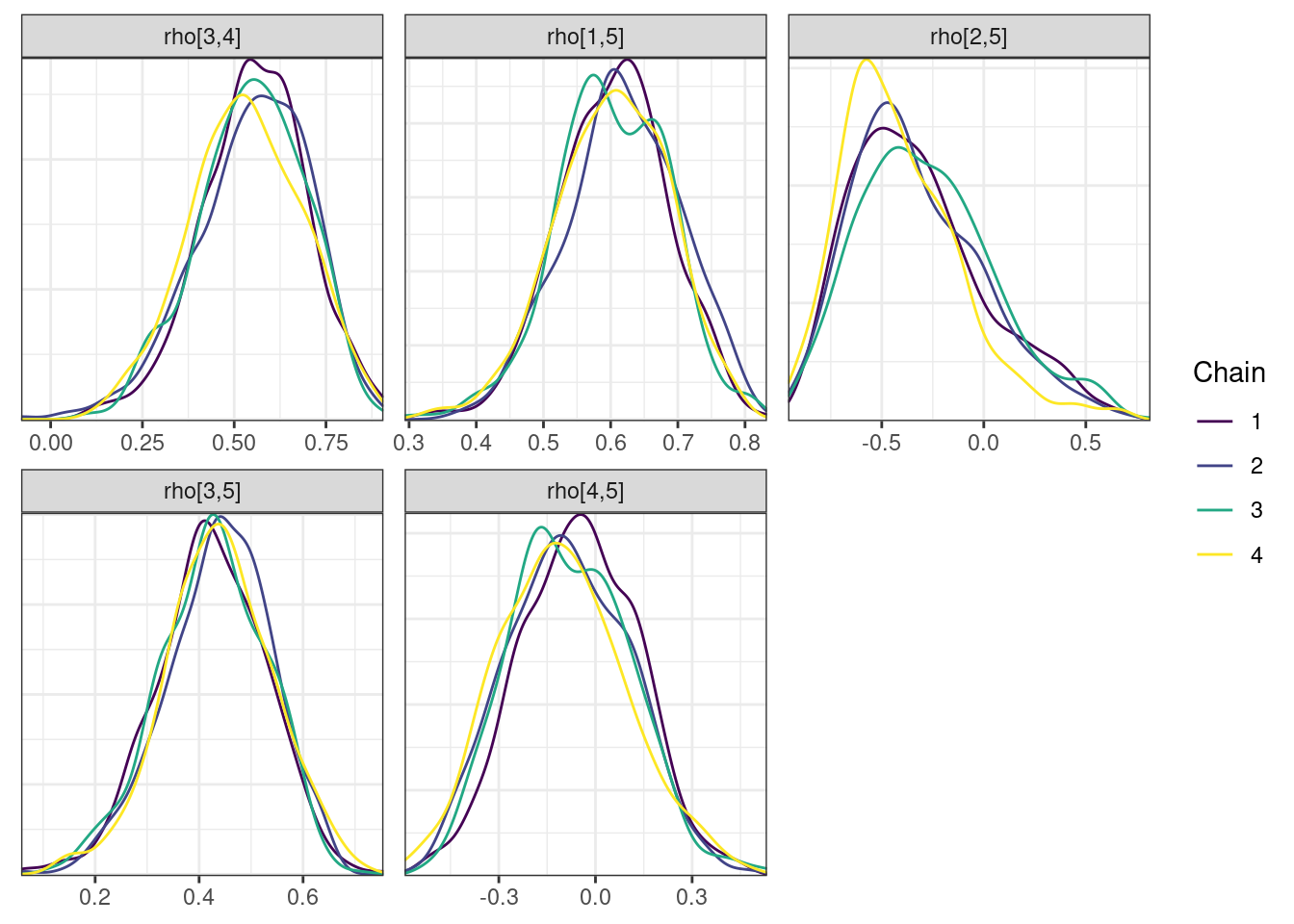
Figure 5: MCMC density plots for model ppkexpo2.

Figure 6: MCMC density plots for model ppkexpo2.

Figure 7: MCMC density plots for model ppkexpo2.

Figure 8: MCMC density plots for model ppkexpo2.

The non-centered parameterization substantially improved the sampling performance and eliminated the divergent transitions.

Revised model—incorporate allometric scaling

Now, let’s start to incorporate covariates. For ppkexpo3, we add allometric scaling to the clearance and volume parameters. The model revision process proceeds as before except now we build on ppkexpo2 instead of ppkexpo1.

ppkexpo3 <- copy_model_from(ppkexpo2, "ppkexpo3", .inherit_tags = TRUE, 
                      .overwrite = TRUE) %>%
  add_tags(TAGS$allometric) %>%
  add_description("PopPK model: ppkexpo2 + allometric scaling")

Now, manually edit ppkexpo3.stan and ppkexpo3-standata.R to implement allometric scaling and add body weight to the data set.

For this demo, we’ll copy previously created files from the demo folder.

ppkexpo3 <- ppkexpo3 %>%
  add_stanmod_file(here(MODEL_DIR, "demo", "ppkexpo3.stan")) %>%
  add_standata_file(here(MODEL_DIR, "demo", "ppkexpo3-standata.R"))

Here is the revised Stan model with allometric scaling.

. /*
. Base PPK model
.   - Linear 2 compartment
.   - Non-centered parameterization
.   - lognormal residual variation
.   - Allometric scaling
.   
. Based on NONMEM PopPK FOCE example project
. */
. 
. data{
.   int<lower = 1> nId; // number of individuals
.   int<lower = 1> nt; // number of events (rows in data set)
.   int<lower = 1> nObs; // number of PK observations
.   array[nObs] int<lower = 1> iObs; // event indices for PK observations
.   int<lower = 1> nBlq; // number of BLQ observations
.   array[nBlq] int<lower = 1> iBlq; // event indices for BLQ observations
.   array[nt] real<lower = 0> amt, time;
.   array[nt] int<lower = 1> cmt;
.   array[nt] int<lower = 0> evid;
.   array[nId] int<lower = 1> start, end; // indices of first & last observations
.   vector<lower = 0>[nId] weight;
.   vector<lower = 0>[nObs] cObs;
.   real<lower = 0> LOQ;
. }
. 
. transformed data{
.   int<lower = 1> nRandom = 5, nCmt = 3;
.   array[nt] real<lower = 0> rate = rep_array(0.0, nt), 
.                             ii = rep_array(0.0, nt);
.   array[nt] int<lower = 0> addl = rep_array(0, nt), 
.                            ss = rep_array(0, nt);
.   array[nId, nCmt] real F = rep_array(1.0, nId, nCmt), 
.                         tLag = rep_array(0.0, nId, nCmt);
.   }
. 
. parameters{
.   real<lower = 0> CLHat, QHat, V2Hat, V3Hat;
. // To constrain kaHat > lambda1 uncomment the following
.   real<lower = (CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat +
.       sqrt((CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat)^2 -
.            4 * CLHat / V2Hat * QHat / V3Hat)) / 2> kaHat; // ka > lambda_1
.   
.   real<lower = 0> sigma;
.   vector<lower = 0>[nRandom] omega;
. //  corr_matrix[nRandom] rho;
. //  array[nId] vector[nRandom] theta;
.   cholesky_factor_corr[nRandom] L_corr;
.   matrix[nRandom, nId] z;
. }
. 
. transformed parameters{
.   vector[nRandom] thetaHat = log([CLHat, QHat, V2Hat, V3Hat, kaHat]');
.   // Individual parameters
.   matrix[nId, nRandom] theta = (rep_matrix(thetaHat, nId) + diag_pre_multiply(omega, L_corr * z))';
.   vector<lower = 0>[nId] CL = exp(theta[,1] + 0.75 * log(weight / 70)),
.                          Q = exp(theta[,2] + 0.75 * log(weight / 70)),
.                          V2 = exp(theta[,3] + log(weight / 70)),
.                          V3 = exp(theta[,4] + log(weight / 70)),
.                          ka = exp(theta[,5]);
.   corr_matrix[nRandom] rho =  L_corr * L_corr';
. 
.   row_vector[nt] cHat; // predicted concentration
.   matrix[nCmt, nt] x; // mass in all compartments
.   
.   for(j in 1:nId){
.     x[, start[j]:end[j]] = pmx_solve_twocpt(time[start[j]:end[j]],
.                                             amt[start[j]:end[j]],
.                                             rate[start[j]:end[j]],
.                                             ii[start[j]:end[j]],
.                                             evid[start[j]:end[j]],
.                                             cmt[start[j]:end[j]],
.                                             addl[start[j]:end[j]],
.                                             ss[start[j]:end[j]],
.                                             {CL[j], Q[j], V2[j], V3[j], ka[j]});
. 
.     cHat[start[j]:end[j]] = x[2, start[j]:end[j]] / V2[j];
.   }
. }
. 
. model{
.   // priors
.   CLHat ~ normal(0, 10); 
.   QHat ~ normal(0, 10);
.   V2Hat ~ normal(0, 50);
.   V3Hat ~ normal(0, 100);
.   kaHat ~ normal(0, 3);
.   sigma ~ normal(0, 0.5);
.   omega ~ normal(0, 0.5); 
.   L_corr ~ lkj_corr_cholesky(2);
.   
.   // interindividual variability
.   to_vector(z) ~ normal(0, 1);
. 
.   // likelihood
.   cObs ~ lognormal(log(cHat[iObs]), sigma); // observed data likelihood
.   target += lognormal_lcdf(LOQ | log(cHat[iBlq]), sigma); // BLQ data likelihood
. 
. }
. 
. generated quantities{
.   // Individual parameters for hypothetical new individuals
.   matrix[nRandom, nId] zNew;
.   matrix[nId, nRandom] thetaNew;
.   vector<lower = 0>[nId] CLNew, QNew, V2New, V3New, kaNew;
. 
.   row_vector[nt] cHatNew; // predicted concentration in new individuals
.   matrix[nCmt, nt] xNew; // mass in all compartments in new individuals
.   array[nt] real cPred, cPredNew;
. 
.   vector[nObs + nBlq] log_lik;
. 
.   // Simulations for posterior predictive checks
.   for(j in 1:nId){
.     zNew[,j] = to_vector(normal_rng(rep_vector(0, nRandom), 1));
.   }
.   thetaNew = (rep_matrix(thetaHat, nId) + diag_pre_multiply(omega, L_corr * zNew))';
.   CLNew = exp(thetaNew[,1] + 0.75 * log(weight / 70));
.   QNew = exp(thetaNew[,2] + 0.75 * log(weight / 70));
.   V2New = exp(thetaNew[,3] + log(weight / 70));
.   V3New = exp(thetaNew[,4] + log(weight / 70));
.   kaNew = exp(thetaNew[,5]);
. 
.   for(j in 1:nId){
.     xNew[, start[j]:end[j]] = pmx_solve_twocpt(time[start[j]:end[j]],
.                                                amt[start[j]:end[j]],
.                                                rate[start[j]:end[j]],
.                                                ii[start[j]:end[j]],
.                                                evid[start[j]:end[j]],
.                                                cmt[start[j]:end[j]],
.                                                addl[start[j]:end[j]],
.                                                ss[start[j]:end[j]],
.                                                {CLNew[j], QNew[j], V2New[j], 
.                                                V3New[j], kaNew[j]});
. 
.     cHatNew[start[j]:end[j]] = xNew[2, start[j]:end[j]] / V2New[j];
. 
.     
.     cPred[start[j]] = 0.0;
.     cPredNew[start[j]] = 0.0;
.     // new observations in existing individuals
.     cPred[(start[j] + 1):end[j]] = lognormal_rng(log(cHat[(start[j] + 1):end[j]]), 
.       sigma);
.     // new observations in new individuals
.     cPredNew[(start[j] + 1):end[j]] = lognormal_rng(log(cHatNew[(start[j] + 1):end[j]]), 
.       sigma); 
.   }
.   
.   // Calculate log-likelihood values to use for LOO CV
.   
.   // Observation-level log-likelihood
.   for(i in 1:nObs)
.     log_lik[i] = lognormal_lpdf(cObs[i] | log(cHat[iObs[i]]), sigma);
.   for(i in 1:nBlq)
.     log_lik[i + nObs] = lognormal_lcdf(LOQ | log(cHat[iBlq[i]]), sigma);
.     
. }

ppkexpo3: Submit the model

## Set cmdstanr arguments
ppkexpo3 <- ppkexpo3 %>%
  set_stanargs(list(iter_warmup = 500,
                    iter_sampling = 500,
                    thin = 1,
                    chains = 4,
                    parallel_chains = 4,
##                    refresh = 10,
                    seed = 1234,
                    save_warmup = FALSE),
               .clear = TRUE)

## Check that the necessary files are present
check_stan_model(ppkexpo3)

## Fit the model using Stan
ppkexpo3_fit <- ppkexpo3 %>% submit_model(.overwrite = TRUE)

ppkexpo3: Parameter summary and sampling diagnostics

model_name <- "ppkexpo3"
mod <- read_model(here(MODEL_DIR, model_name))
fit <- read_fit_model(mod)

fit$cmdstan_diagnose()
. Processing csv files: /data/expo4-torsten-poppk/model/stan/ppkexpo3/ppkexpo3-output/ppkexpo3-202409271857-1-8ae134.csv, /data/expo4-torsten-poppk/model/stan/ppkexpo3/ppkexpo3-output/ppkexpo3-202409271857-2-8ae134.csv, /data/expo4-torsten-poppk/model/stan/ppkexpo3/ppkexpo3-output/ppkexpo3-202409271857-3-8ae134.csv, /data/expo4-torsten-poppk/model/stan/ppkexpo3/ppkexpo3-output/ppkexpo3-202409271857-4-8ae134.csv
. 
. Checking sampler transitions treedepth.
. Treedepth satisfactory for all transitions.
. 
. Checking sampler transitions for divergences.
. No divergent transitions found.
. 
. Checking E-BFMI - sampler transitions HMC potential energy.
. E-BFMI satisfactory.
. 
. Effective sample size satisfactory.
. 
. The following parameters had split R-hat greater than 1.05:
.   CLHat, L_corr[3,2], L_corr[5,2], L_corr[3,3], L_corr[5,4], z[2,4], z[2,24], z[2,25], z[2,27], z[2,46], z[2,50], z[2,52], z[2,62], z[2,63], z[2,64], z[2,66], z[2,68], z[2,76], z[2,86], z[2,92], z[2,93], z[2,101], z[2,111], z[2,117], z[2,135], z[2,144], z[2,147], z[2,150], z[2,154], thetaHat[1], theta[46,2], theta[86,2], theta[147,2], Q[46], Q[86], Q[147], rho[3,2], rho[2,3], rho[5,4], rho[4,5]
. Such high values indicate incomplete mixing and biased estimation.
. You should consider regularizating your model with additional prior information or a more effective parameterization.
. 
. Processing complete.
pars <- c("lp__", "CLHat", "QHat", "V2Hat", "V3Hat", "kaHat",
          "sigma", glue("omega[{1:5}]"),
          paste0("rho[", matrix(apply(expand.grid(1:5, 1:5),
                                      1, paste, collapse = ","),
                                ncol = 5)[upper.tri(diag(5), 
                                                    diag = FALSE)], "]"))
# Get posterior samples for parameters of interest
posterior <- fit$draws(variables = pars)
# Get quantities related to NUTS performance, e.g., occurrence of
# divergent transitions
np <- nuts_params(fit) 

n_iter <- dim(posterior)[1]
n_chains <- dim(posterior)[2]

ptable <- fit$summary(variables = pars) %>%
  mutate(across(-variable, ~ pmtables::sig(.x, maxex = 4))) %>% 
  rename(parameter = variable) %>%
  mutate("90% CI" = paste("(", q5, ", ", q95, ")", 
                          sep = "")) %>%
  select(parameter, mean, median, sd, mad, "90% CI", ess_bulk, ess_tail, rhat)

ptable %>% 
  kable %>%
  kable_styling()
parameter mean median sd mad 90% CI ess_bulk ess_tail rhat
lp__ -32.2 -31.6 27.0 27.1 (-77.5, 11.8) 408 984 1.00
CLHat 3.13 3.13 0.100 0.102 (2.97, 3.29) 46.4 162 1.07
QHat 3.77 3.77 0.170 0.166 (3.51, 4.06) 672 1090 1.01
V2Hat 61.7 61.8 1.81 1.87 (58.8, 64.7) 69.3 534 1.04
V3Hat 67.8 67.8 1.64 1.64 (65.1, 70.5) 1810 1410 1.00
kaHat 1.63 1.63 0.116 0.114 (1.45, 1.84) 374 1020 1.01
sigma 0.213 0.213 0.00305 0.00307 (0.209, 0.218) 2520 1420 1.00
omega[1] 0.407 0.407 0.0217 0.0215 (0.375, 0.446) 157 402 1.01
omega[2] 0.0831 0.0791 0.0535 0.0590 (0.00648, 0.176) 471 1090 1.01
omega[3] 0.291 0.290 0.0224 0.0221 (0.258, 0.331) 326 576 1.01
omega[4] 0.0431 0.0365 0.0309 0.0324 (0.00424, 0.101) 301 626 1.01
omega[5] 0.528 0.526 0.0633 0.0621 (0.426, 0.638) 591 1060 1.01
rho[1,2] -0.273 -0.312 0.312 0.299 (-0.716, 0.327) 1660 1440 1.00
rho[1,3] 0.618 0.621 0.0650 0.0640 (0.508, 0.719) 486 869 1.01
rho[2,3] -0.184 -0.203 0.346 0.368 (-0.715, 0.422) 20.4 76.6 1.14
rho[1,4] 0.0452 0.0415 0.305 0.298 (-0.470, 0.568) 1970 1070 1.00
rho[2,4] 0.0185 0.0261 0.349 0.371 (-0.566, 0.577) 1280 1320 1.00
rho[3,4] 0.0393 0.0314 0.314 0.321 (-0.485, 0.553) 1810 1310 1.00
rho[1,5] 0.641 0.645 0.0806 0.0798 (0.501, 0.763) 638 1290 1.01
rho[2,5] -0.292 -0.348 0.335 0.328 (-0.761, 0.330) 70.0 292 1.05
rho[3,5] 0.520 0.526 0.0979 0.0955 (0.348, 0.675) 558 1250 1.01
rho[4,5] -0.0585 -0.0860 0.334 0.343 (-0.587, 0.534) 52.4 242 1.05

Trace and density plots

Next, we look at the trace and density plots.

mcmc_history_plots <- mcmc_history(posterior,
                                  nParPerPage = 6, 
                                  np = np)
mcmc_history_plots
. [[1]]
. 
. [[2]]
. 
. [[3]]
. 
. [[4]]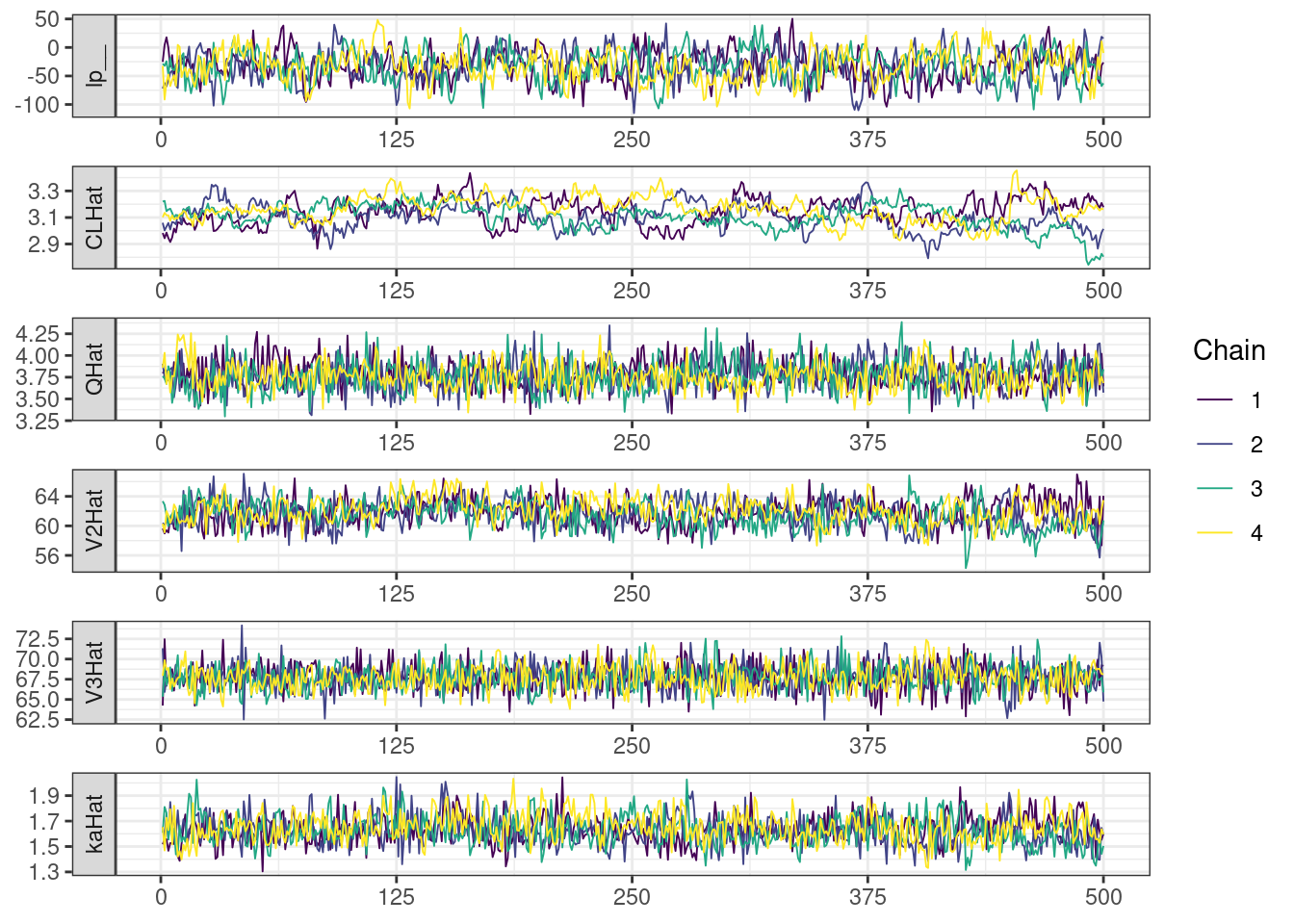

Figure 9: MCMC trace plots for model ppkexpo3.

Figure 10: MCMC trace plots for model ppkexpo3.

Figure 11: MCMC trace plots for model ppkexpo3.

Figure 12: MCMC trace plots for model ppkexpo3.
  mcmc_density_chain_plots <- mcmc_density(posterior, 
                                           nParPerPage = 6, byChain = TRUE)
mcmc_density_chain_plots
. [[1]]
. 
. [[2]]
. 
. [[3]]
. 
. [[4]]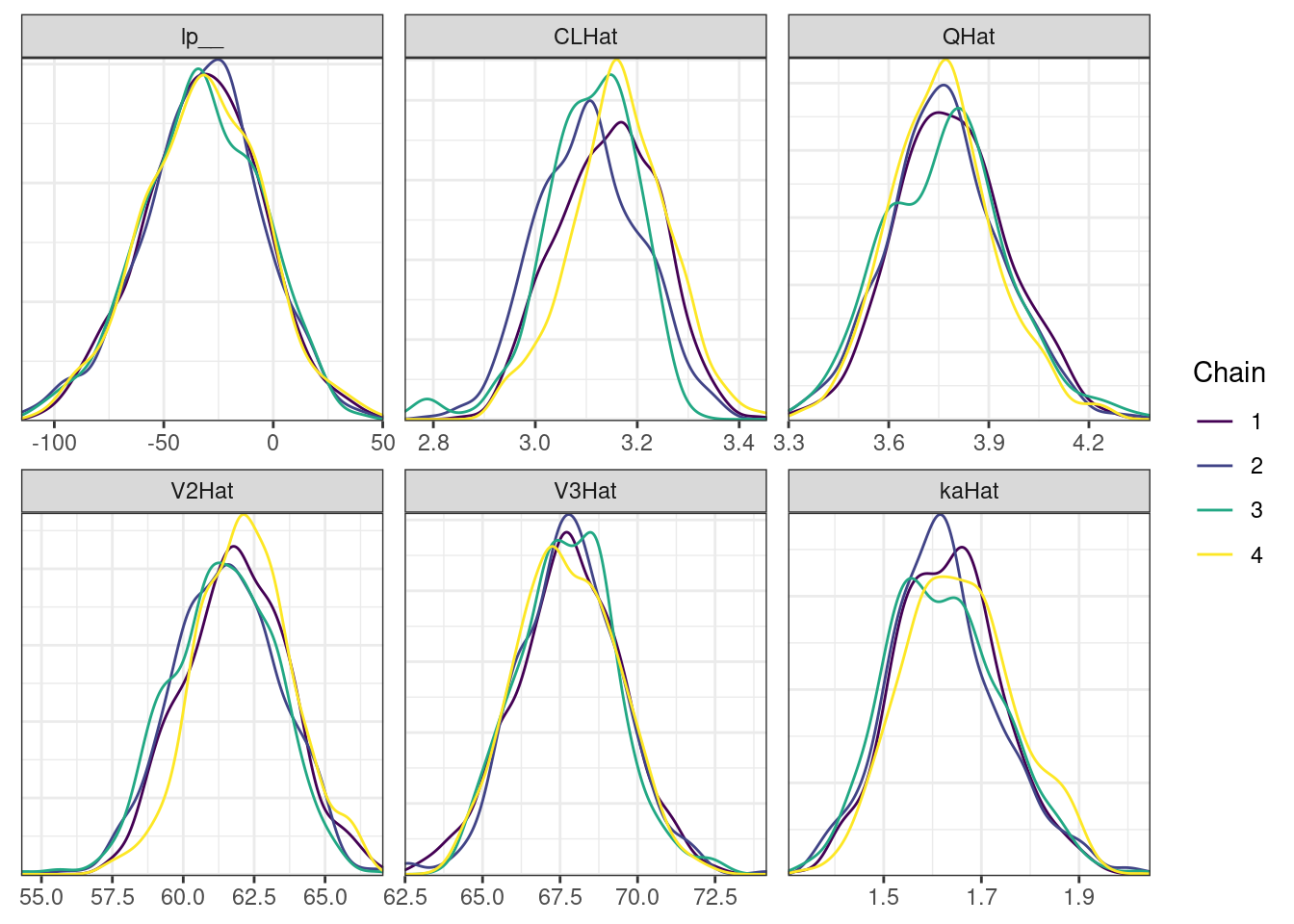

Figure 13: MCMC density plots for model ppkexpo3.

Figure 14: MCMC density plots for model ppkexpo3.

Figure 15: MCMC density plots for model ppkexpo3.

Figure 16: MCMC density plots for model ppkexpo3.

There is little or no decrease in the overall log probability (lp__), which suggests the addition of allometric scaling did not markedly improve the model fit. lp__ is a relatively crude metric for model comparison. We’ll discuss better metrics in a subsequent section. The sampling performance deteriorated somewhat comparatively to ppkexpo2, particularly with respect to \(\widehat{CL}\).

Revised model—incorporate additional covariates

Let’s incorporate additional covariate effects. Specifically, we add effects of eGFR, age, and albumin on clearance (CL).

ppkexpo4 <- copy_model_from(ppkexpo3, "ppkexpo4", .inherit_tags = TRUE, 
                      .overwrite = TRUE) %>%
  add_tags(with(TAGS, c(EGFR_CL, age_CL, albumin_CL))) %>%
  add_description("PopPK model: ppkexpo3 + allometric scaling & effects of EGFR, age, and albumin in CL")

Now, manually edit ppkexpo4.stan and ppkexpo4-standata.R to implement the effects of eGFR, age, and albumin on CL, and add those covariates to the data set. We also need to revise the initial estimates to include coefficients for these additional covariates.

For this demo, copy the previously created files from the demo folder.

ppkexpo4 <- ppkexpo4 %>%
  add_stanmod_file(here(MODEL_DIR, "demo", "ppkexpo4.stan")) %>%
  add_standata_file(here(MODEL_DIR, "demo", "ppkexpo4-standata.R")) %>%
  add_staninit_file(here(MODEL_DIR, "demo", "ppkexpo4-init.R"))

Here is the Stan model incorporating the effects of eGFR, age, and albumin on CL.

. /*
. Final PPK model
.   - Linear 2 compartment
.   - Non-centered parameterization
.   - lognormal residual variation
.   - Allometric scaling
.   - Additional covariates: EGFR, age, albumin
.   
. Based on NONMEM PopPK FOCE example project
. */
. 
. data{
.   int<lower = 1> nId; // number of individuals
.   int<lower = 1> nt; // number of events (rows in data set)
.   int<lower = 1> nObs; // number of PK observations
.   array[nObs] int<lower = 1> iObs; // event indices for PK observations
.   int<lower = 1> nBlq; // number of BLQ observations
.   array[nBlq] int<lower = 1> iBlq; // event indices for BLQ observations
.   array[nt] real<lower = 0> amt, time;
.   array[nt] int<lower = 1> cmt;
.   array[nt] int<lower = 0> evid;
.   array[nId] int<lower = 1> start, end; // indices of first & last observations
.   vector<lower = 0>[nId] weight, EGFR, age, albumin;
.   vector<lower = 0>[nObs] cObs;
.   real<lower = 0> LOQ;
. }
. 
. transformed data{
.   int<lower = 1> nRandom = 5, nCmt = 3;
.   array[nt] real<lower = 0> rate = rep_array(0.0, nt), 
.                             ii = rep_array(0.0, nt);
.   array[nt] int<lower = 0> addl = rep_array(0, nt), 
.                            ss = rep_array(0, nt);
.   array[nId, nCmt] real F = rep_array(1.0, nId, nCmt), 
.                         tLag = rep_array(0.0, nId, nCmt);
.   }
. 
. parameters{
.   real<lower = 0> CLHat, QHat, V2Hat, V3Hat;
. // To constrain kaHat > lambda1 uncomment the following
.   real<lower = (CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat +
.       sqrt((CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat)^2 -
.            4 * CLHat / V2Hat * QHat / V3Hat)) / 2> kaHat; // ka > lambda_1
.   real EGFR_CL, age_CL, albumin_CL;
.   
.   real<lower = 0> sigma;
.   vector<lower = 0>[nRandom] omega;
. //  corr_matrix[nRandom] rho;
. //  array[nId] vector[nRandom] theta;
.   cholesky_factor_corr[nRandom] L_corr;
.   matrix[nRandom, nId] z;
. }
. 
. transformed parameters{
.   vector[nRandom] thetaHat = log([CLHat, QHat, V2Hat, V3Hat, kaHat]');
.   // Individual parameters
.   matrix[nId, nRandom] theta = (rep_matrix(thetaHat, nId) + diag_pre_multiply(omega, L_corr * z))';
.   vector<lower = 0>[nId] CL = exp(theta[,1] + 0.75 * log(weight / 70) +
.                               EGFR_CL * log(EGFR / 90) +
.                               age_CL * log(age / 35) +
.                               albumin_CL * log(albumin / 4.5)),
.                          Q = exp(theta[,2] + 0.75 * log(weight / 70)),
.                          V2 = exp(theta[,3] + log(weight / 70)),
.                          V3 = exp(theta[,4] + log(weight / 70)),
.                          ka = exp(theta[,5]);
.   corr_matrix[nRandom] rho =  L_corr * L_corr';
. 
.   row_vector[nt] cHat; // predicted concentration
.   matrix[nCmt, nt] x; // mass in all compartments
.   
.   for(j in 1:nId){
.     x[, start[j]:end[j]] = pmx_solve_twocpt(time[start[j]:end[j]],
.                                             amt[start[j]:end[j]],
.                                             rate[start[j]:end[j]],
.                                             ii[start[j]:end[j]],
.                                             evid[start[j]:end[j]],
.                                             cmt[start[j]:end[j]],
.                                             addl[start[j]:end[j]],
.                                             ss[start[j]:end[j]],
.                                             {CL[j], Q[j], V2[j], V3[j], ka[j]});
. 
.     cHat[start[j]:end[j]] = x[2, start[j]:end[j]] / V2[j];
.   }
. }
. 
. model{
.   // priors
.   CLHat ~ normal(0, 10); 
.   QHat ~ normal(0, 10);
.   V2Hat ~ normal(0, 50);
.   V3Hat ~ normal(0, 100);
.   kaHat ~ normal(0, 3);
.   EGFR_CL ~ normal(0, 2);
.   age_CL ~ normal(0, 2);
.   albumin_CL ~ normal(0, 2);
.   
.   sigma ~ normal(0, 0.5);
.   omega ~ normal(0, 0.5); 
.   L_corr ~ lkj_corr_cholesky(2);
.   
.   // interindividual variability
.   to_vector(z) ~ std_normal();
. 
.   // likelihood
.   cObs ~ lognormal(log(cHat[iObs]), sigma); // observed data likelihood
.   target += lognormal_lcdf(LOQ | log(cHat[iBlq]), sigma); // BLQ data likelihood
. 
. }
. 
. generated quantities{
.   // Individual parameters for hypothetical new individuals
.   matrix[nRandom, nId] zNew;
.   matrix[nId, nRandom] thetaNew;
.   vector<lower = 0>[nId] CLNew, QNew, V2New, V3New, kaNew;
. 
.   row_vector[nt] cHatNew; // predicted concentration in new individuals
.   matrix[nCmt, nt] xNew; // mass in all compartments in new individuals
.   array[nt] real cPred, cPredNew;
. 
.   vector[nObs + nBlq] log_lik;
. 
.   // Simulations for posterior predictive checks
.   for(j in 1:nId){
.     zNew[,j] = to_vector(normal_rng(rep_vector(0, nRandom), 1));
.   }
.   thetaNew = (rep_matrix(thetaHat, nId) + diag_pre_multiply(omega, L_corr * zNew))';
.   CLNew = exp(thetaNew[,1] + 0.75 * log(weight / 70) +
.           EGFR_CL * log(EGFR / 90) +
.           age_CL * log(age / 35) +
.           albumin_CL * log(albumin / 4.5));
.   QNew = exp(thetaNew[,2] + 0.75 * log(weight / 70));
.   V2New = exp(thetaNew[,3] + log(weight / 70));
.   V3New = exp(thetaNew[,4] + log(weight / 70));
.   kaNew = exp(thetaNew[,5]);
. 
.   for(j in 1:nId){
.     xNew[, start[j]:end[j]] = pmx_solve_twocpt(time[start[j]:end[j]],
.                                                amt[start[j]:end[j]],
.                                                rate[start[j]:end[j]],
.                                                ii[start[j]:end[j]],
.                                                evid[start[j]:end[j]],
.                                                cmt[start[j]:end[j]],
.                                                addl[start[j]:end[j]],
.                                                ss[start[j]:end[j]],
.                                                {CLNew[j], QNew[j], V2New[j], 
.                                                V3New[j], kaNew[j]});
. 
.     cHatNew[start[j]:end[j]] = xNew[2, start[j]:end[j]] / V2New[j];
. 
.     
.     cPred[start[j]] = 0.0;
.     cPredNew[start[j]] = 0.0;
.     // new observations in existing individuals
.     cPred[(start[j] + 1):end[j]] = lognormal_rng(log(cHat[(start[j] + 1):end[j]]), 
.       sigma);
.     // new observations in new individuals
.     cPredNew[(start[j] + 1):end[j]] = lognormal_rng(log(cHatNew[(start[j] + 1):end[j]]), 
.       sigma); 
.   }
.   
.   // Calculate log-likelihood values to use for LOO CV
.   
.   // Observation-level log-likelihood
.   for(i in 1:nObs)
.     log_lik[i] = lognormal_lpdf(cObs[i] | log(cHat[iObs[i]]), sigma);
.   for(i in 1:nBlq)
.     log_lik[i + nObs] = lognormal_lcdf(LOQ | log(cHat[iBlq[i]]), sigma);
. 
. }

ppkexpo4: Submit the model

## Set cmdstanr arguments
ppkexpo4 <- ppkexpo4 %>%
  set_stanargs(list(iter_warmup = 500,
                    iter_sampling = 500,
                    thin = 1,
                    chains = 4,
                    parallel_chains = 4,
##                    refresh = 10,
                    seed = 1234,
                    save_warmup = FALSE),
               .clear = TRUE)

## Check that the necessary files are present
check_stan_model(ppkexpo4)

## Fit the model using Stan
ppkexpo4_fit <- ppkexpo4 %>% submit_model(.overwrite = TRUE)

ppkexpo4: Parameter summary and sampling diagnostics

model_name <- "ppkexpo4"
mod <- read_model(here(MODEL_DIR, model_name))
fit <- read_fit_model(mod)

fit$cmdstan_diagnose()
. Processing csv files: /data/expo4-torsten-poppk/model/stan/ppkexpo4/ppkexpo4-output/ppkexpo4-202409272003-1-921811.csv, /data/expo4-torsten-poppk/model/stan/ppkexpo4/ppkexpo4-output/ppkexpo4-202409272003-2-921811.csv, /data/expo4-torsten-poppk/model/stan/ppkexpo4/ppkexpo4-output/ppkexpo4-202409272003-3-921811.csv, /data/expo4-torsten-poppk/model/stan/ppkexpo4/ppkexpo4-output/ppkexpo4-202409272003-4-921811.csv
. 
. Checking sampler transitions treedepth.
. Treedepth satisfactory for all transitions.
. 
. Checking sampler transitions for divergences.
. No divergent transitions found.
. 
. Checking E-BFMI - sampler transitions HMC potential energy.
. E-BFMI satisfactory.
. 
. Effective sample size satisfactory.
. 
. The following parameters had split R-hat greater than 1.05:
.   CLHat, L_corr[3,2], z[2,27], z[2,76], z[2,86], z[2,135], z[2,154], thetaHat[1], rho[3,2], rho[2,3]
. Such high values indicate incomplete mixing and biased estimation.
. You should consider regularizating your model with additional prior information or a more effective parameterization.
. 
. Processing complete.
pars <- c("lp__", "CLHat", "QHat", "V2Hat", "V3Hat", "kaHat",
          "EGFR_CL", "age_CL", "albumin_CL",
          "sigma", glue("omega[{1:5}]"),
          paste0("rho[", matrix(apply(expand.grid(1:5, 1:5),
                                      1, paste, collapse = ","),
                                ncol = 5)[upper.tri(diag(5), 
                                                    diag = FALSE)], "]"))
# Get posterior samples for parameters of interest
posterior <- fit$draws(variables = pars)
# Get quantities related to NUTS performance, e.g., occurrence of
# divergent transitions
np <- nuts_params(fit) 

n_iter <- dim(posterior)[1]
n_chains <- dim(posterior)[2]

ptable <- fit$summary(variables = pars) %>%
  mutate(across(-variable, ~ pmtables::sig(.x, maxex = 4))) %>% 
  rename(parameter = variable) %>%
  mutate("90% CI" = paste("(", q5, ", ", q95, ")", 
                          sep = "")) %>%
  select(parameter, mean, median, sd, mad, "90% CI", ess_bulk, ess_tail, rhat)

ptable %>% 
  kable %>%
  kable_styling()
parameter mean median sd mad 90% CI ess_bulk ess_tail rhat
lp__ -30.0 -30.0 26.3 26.1 (-74.2, 13.3) 398 794 1.01
CLHat 3.28 3.28 0.0869 0.0853 (3.13, 3.42) 131 228 1.06
QHat 3.76 3.77 0.162 0.160 (3.50, 4.04) 1110 1410 1.00
V2Hat 61.7 61.7 1.70 1.72 (58.8, 64.3) 373 572 1.01
V3Hat 67.8 67.8 1.53 1.54 (65.2, 70.3) 1950 1720 0.999
kaHat 1.63 1.62 0.115 0.113 (1.45, 1.82) 605 797 1.01
EGFR_CL 0.494 0.493 0.0513 0.0478 (0.413, 0.582) 228 447 1.02
age_CL -0.0483 -0.0487 0.0750 0.0750 (-0.172, 0.0761) 166 345 1.01
albumin_CL 0.391 0.389 0.0926 0.0945 (0.240, 0.547) 135 370 1.05
sigma 0.213 0.213 0.00292 0.00299 (0.208, 0.218) 1750 1330 1.00
omega[1] 0.345 0.344 0.0199 0.0196 (0.313, 0.379) 233 412 1.01
omega[2] 0.0633 0.0538 0.0458 0.0461 (0.00500, 0.150) 465 729 1.01
omega[3] 0.290 0.289 0.0207 0.0212 (0.258, 0.327) 672 1250 1.01
omega[4] 0.0406 0.0346 0.0298 0.0300 (0.00368, 0.0979) 449 1130 1.00
omega[5] 0.521 0.518 0.0635 0.0638 (0.424, 0.629) 667 1130 1.00
rho[1,2] -0.126 -0.148 0.331 0.351 (-0.632, 0.456) 1760 1230 1.00
rho[1,3] 0.703 0.706 0.0517 0.0493 (0.612, 0.786) 515 1080 1.01
rho[2,3] -0.134 -0.163 0.336 0.352 (-0.643, 0.464) 34.8 236 1.07
rho[1,4] 0.0127 0.0131 0.309 0.319 (-0.509, 0.523) 2260 1420 1.00
rho[2,4] 0.0115 0.0104 0.349 0.380 (-0.558, 0.608) 1110 1690 1.00
rho[3,4] 0.0529 0.0510 0.306 0.318 (-0.460, 0.556) 2350 1560 1.00
rho[1,5] 0.683 0.690 0.0830 0.0815 (0.540, 0.809) 403 758 1.01
rho[2,5] -0.207 -0.240 0.341 0.358 (-0.714, 0.399) 249 562 1.00
rho[3,5] 0.503 0.509 0.0942 0.0940 (0.336, 0.650) 800 1330 1.01
rho[4,5] -0.109 -0.129 0.314 0.334 (-0.598, 0.430) 289 1080 1.00

Trace and density plots

Next, we look at the trace and density plots.

mcmc_history_plots <- mcmc_history(posterior,
                                  nParPerPage = 6, 
                                  np = np)
mcmc_history_plots
. [[1]]
. 
. [[2]]
. 
. [[3]]
. 
. [[4]]
. 
. [[5]]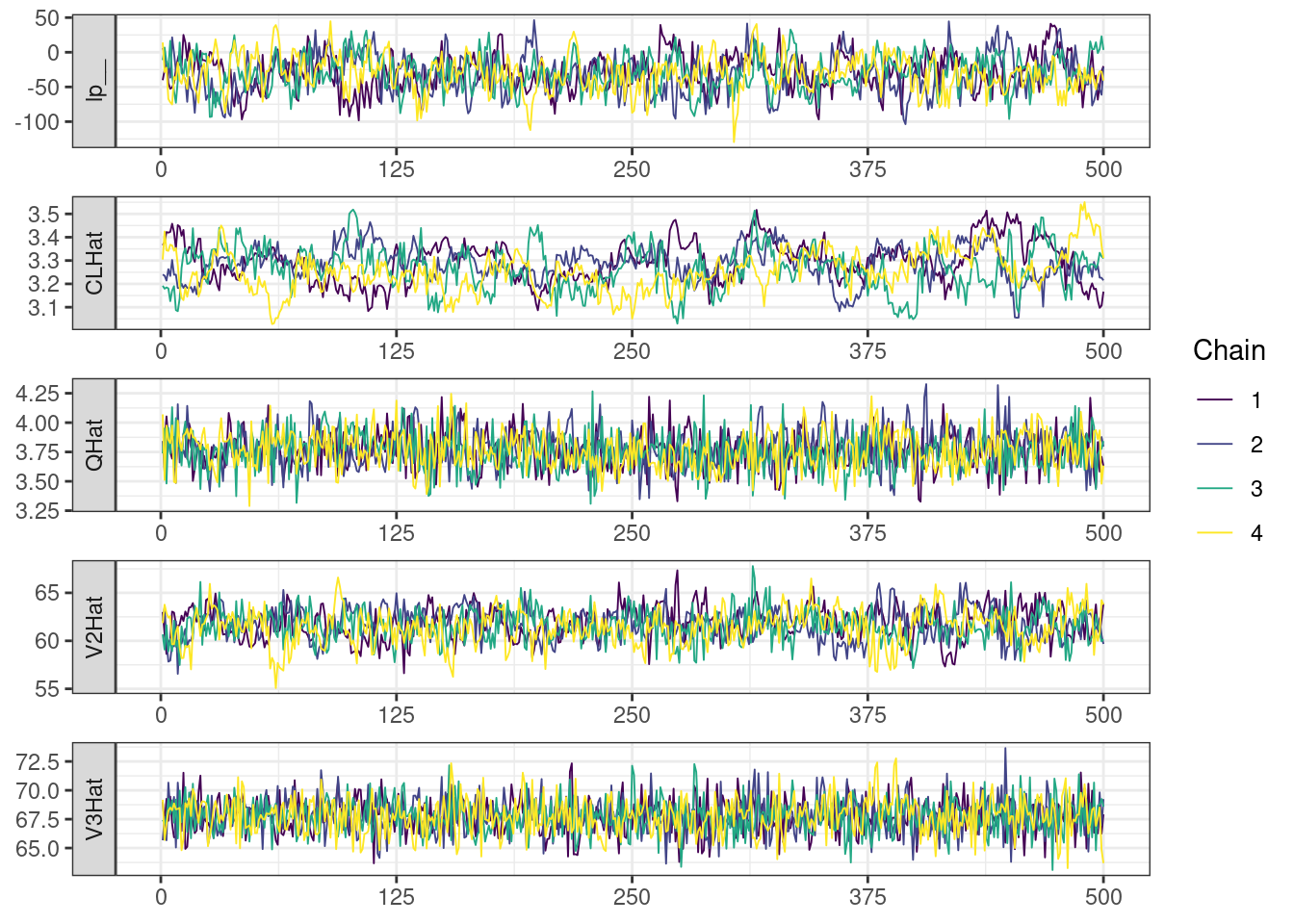

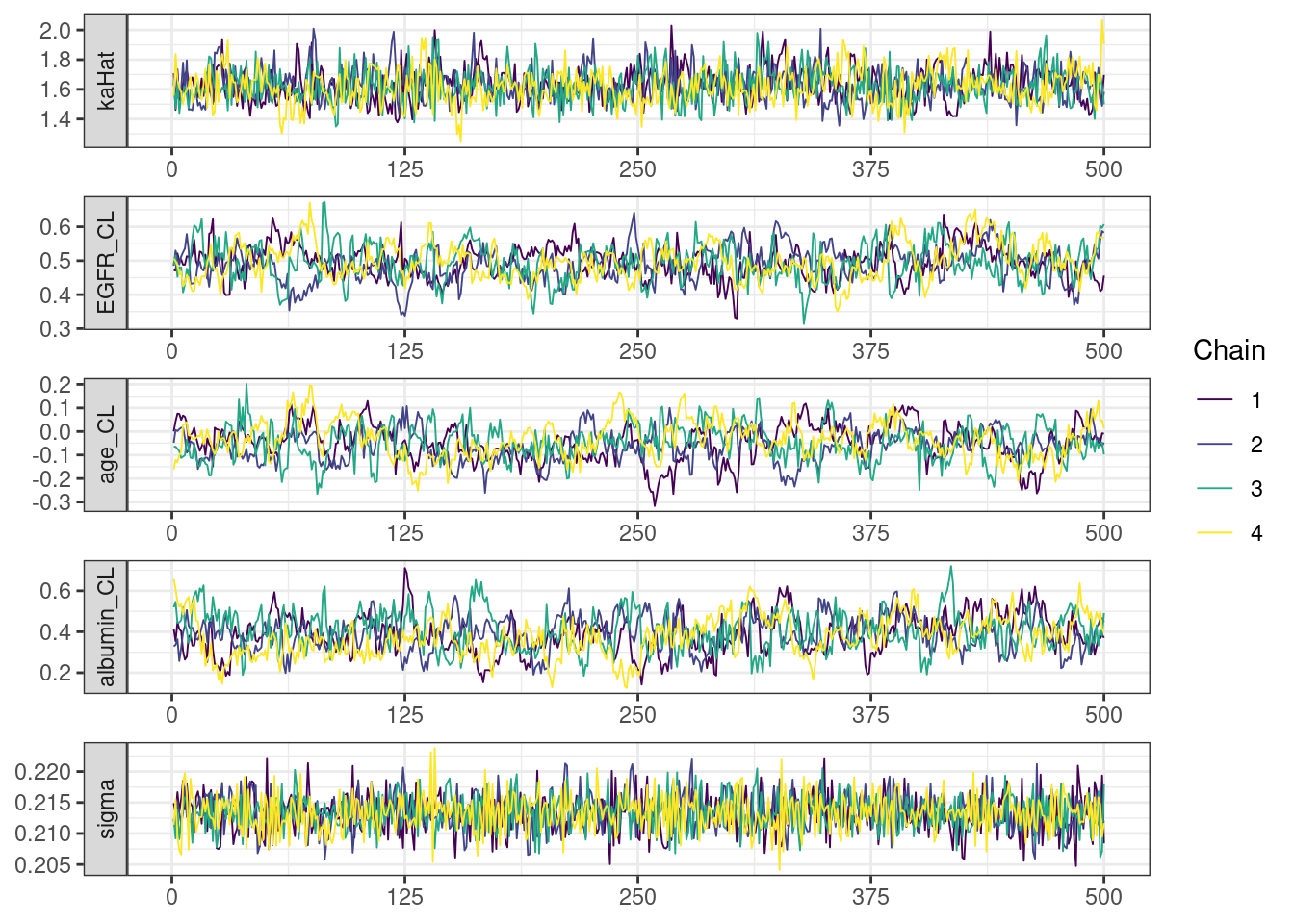
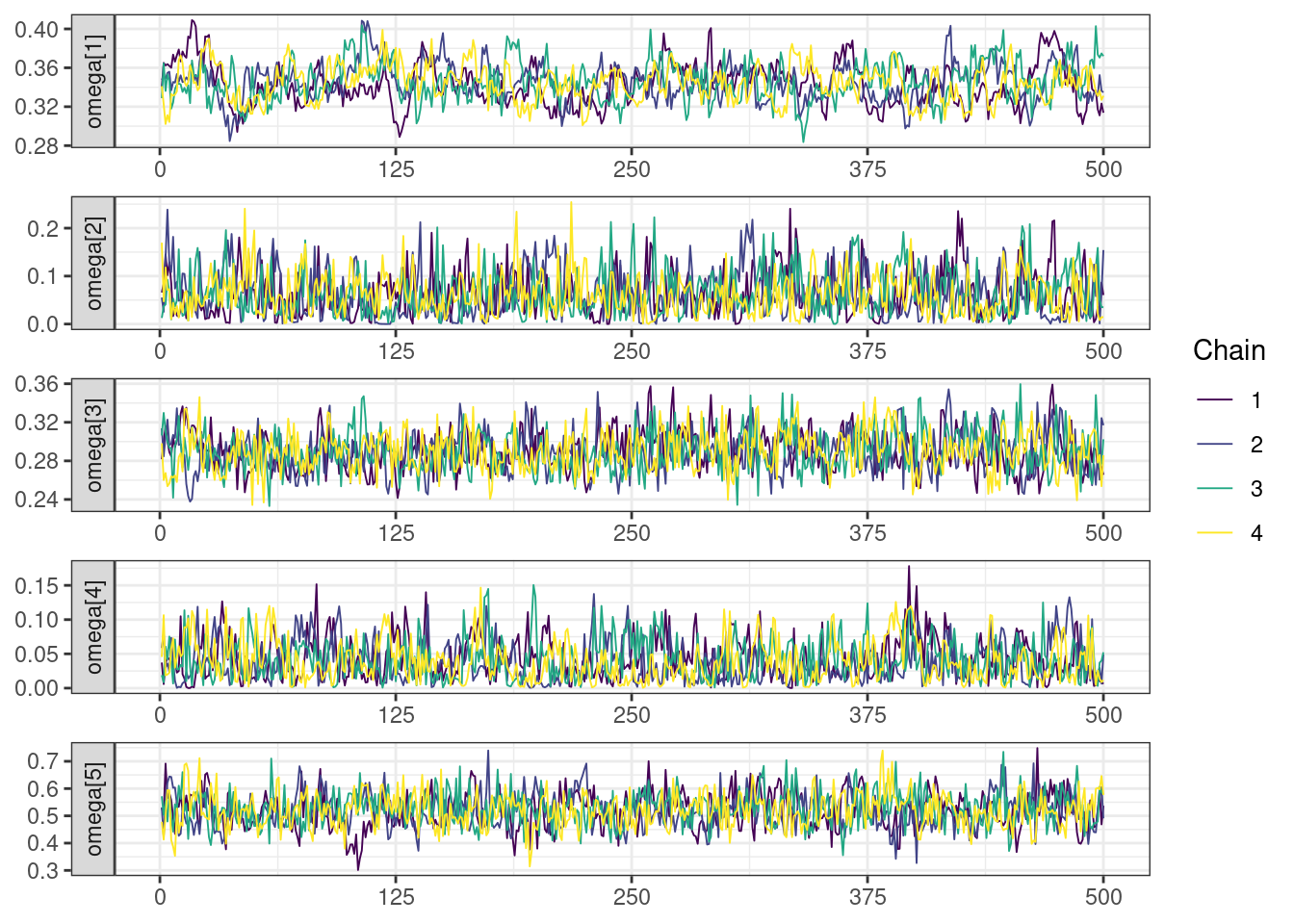
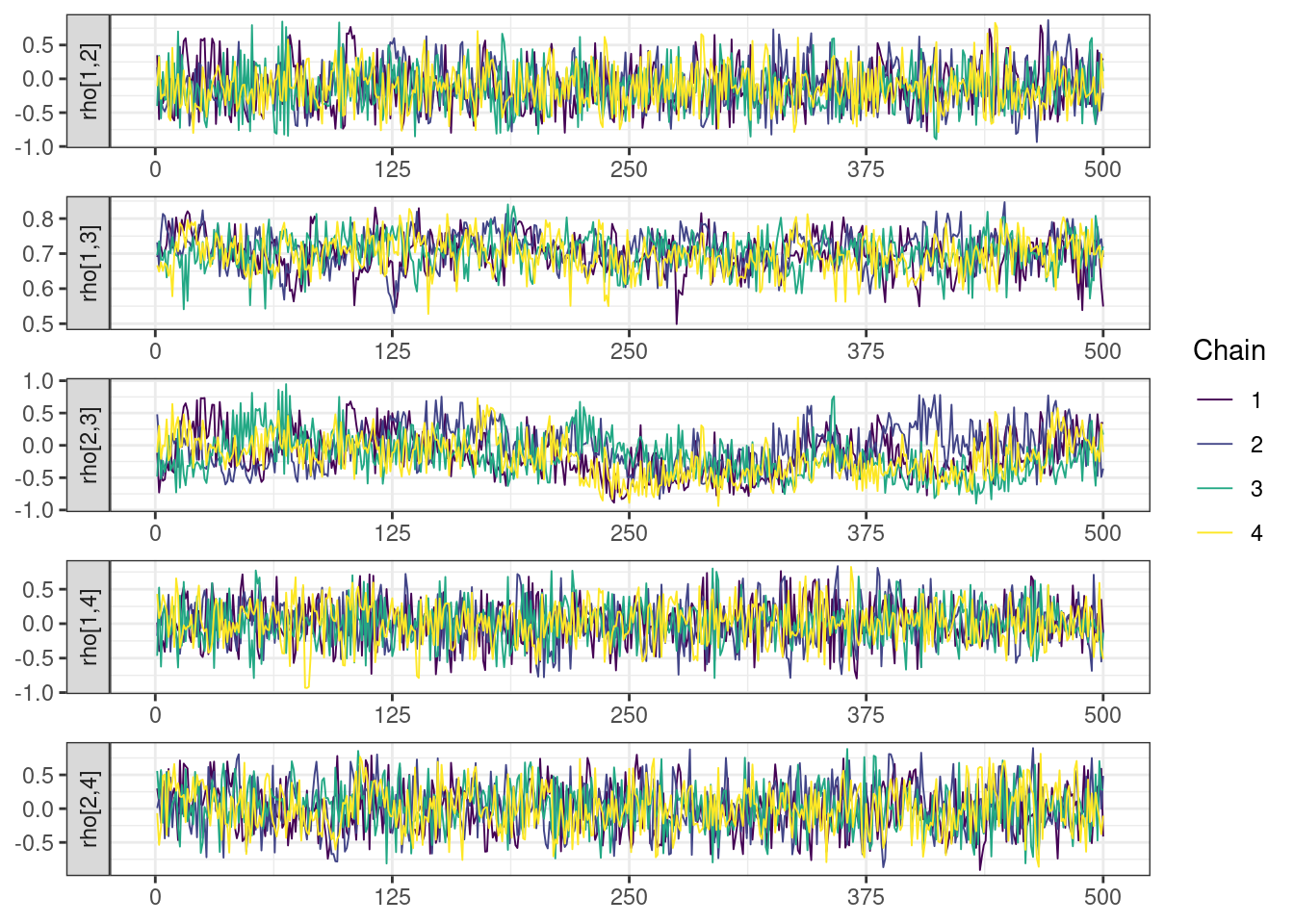
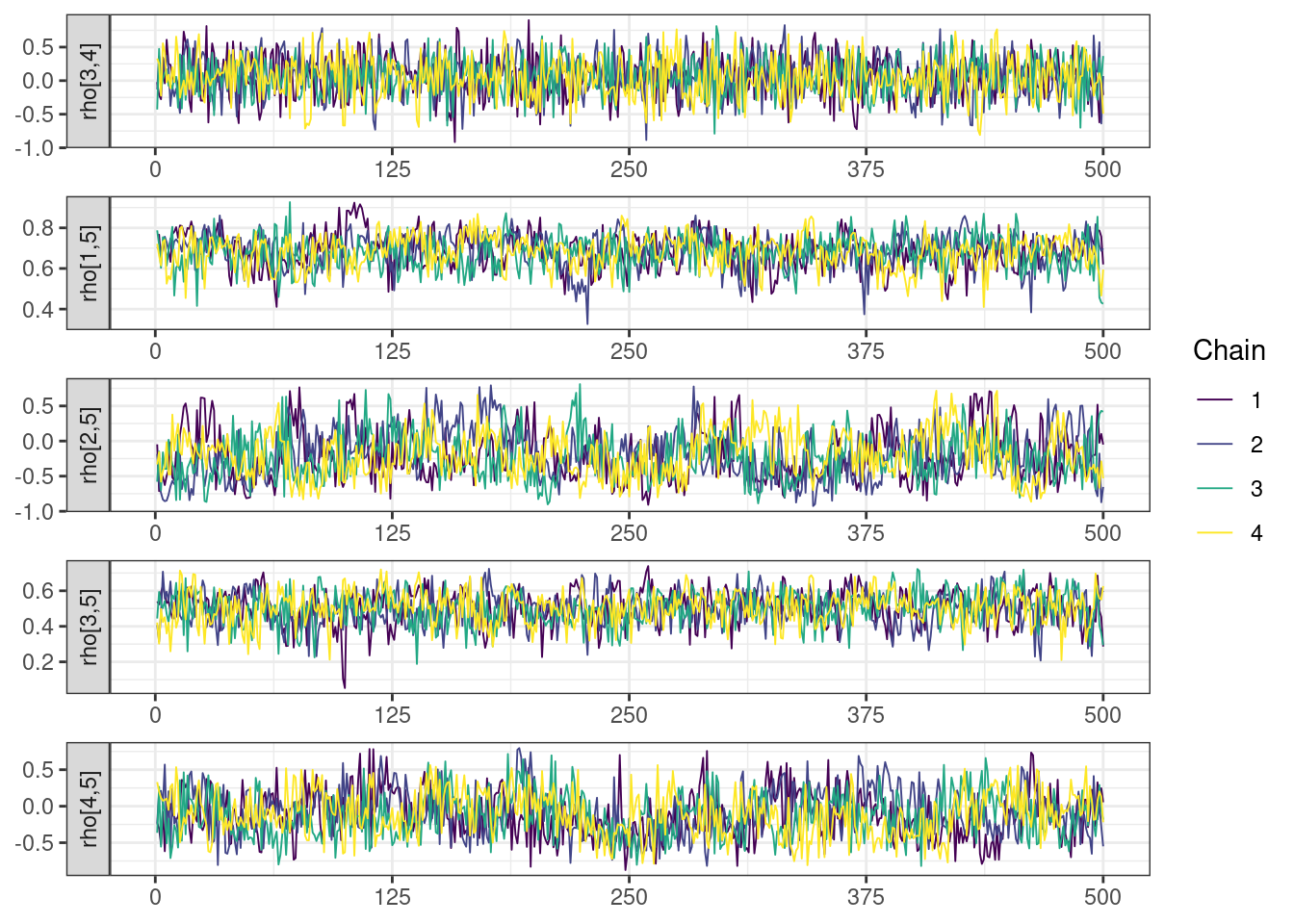
Figure 17: MCMC trace plots for model ppkexpo4.

Figure 18: MCMC trace plots for model ppkexpo4.

Figure 19: MCMC trace plots for model ppkexpo4.

Figure 20: MCMC trace plots for model ppkexpo4.

Figure 21: MCMC trace plots for model ppkexpo4.
  mcmc_density_chain_plots <- mcmc_density(posterior, 
                                           nParPerPage = 6, byChain = TRUE)
mcmc_density_chain_plots
. [[1]]
. 
. [[2]]
. 
. [[3]]
. 
. [[4]]
. 
. [[5]]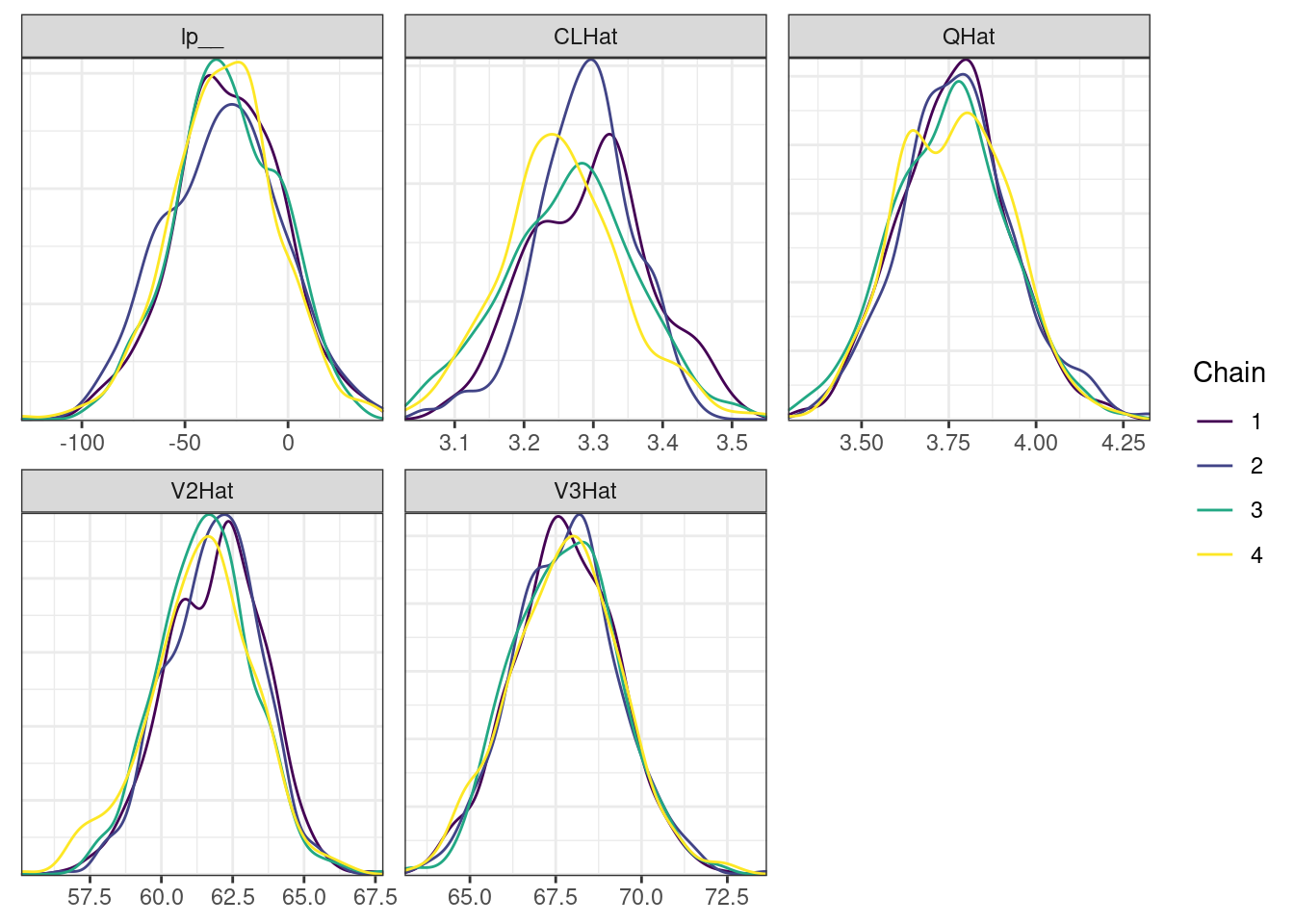

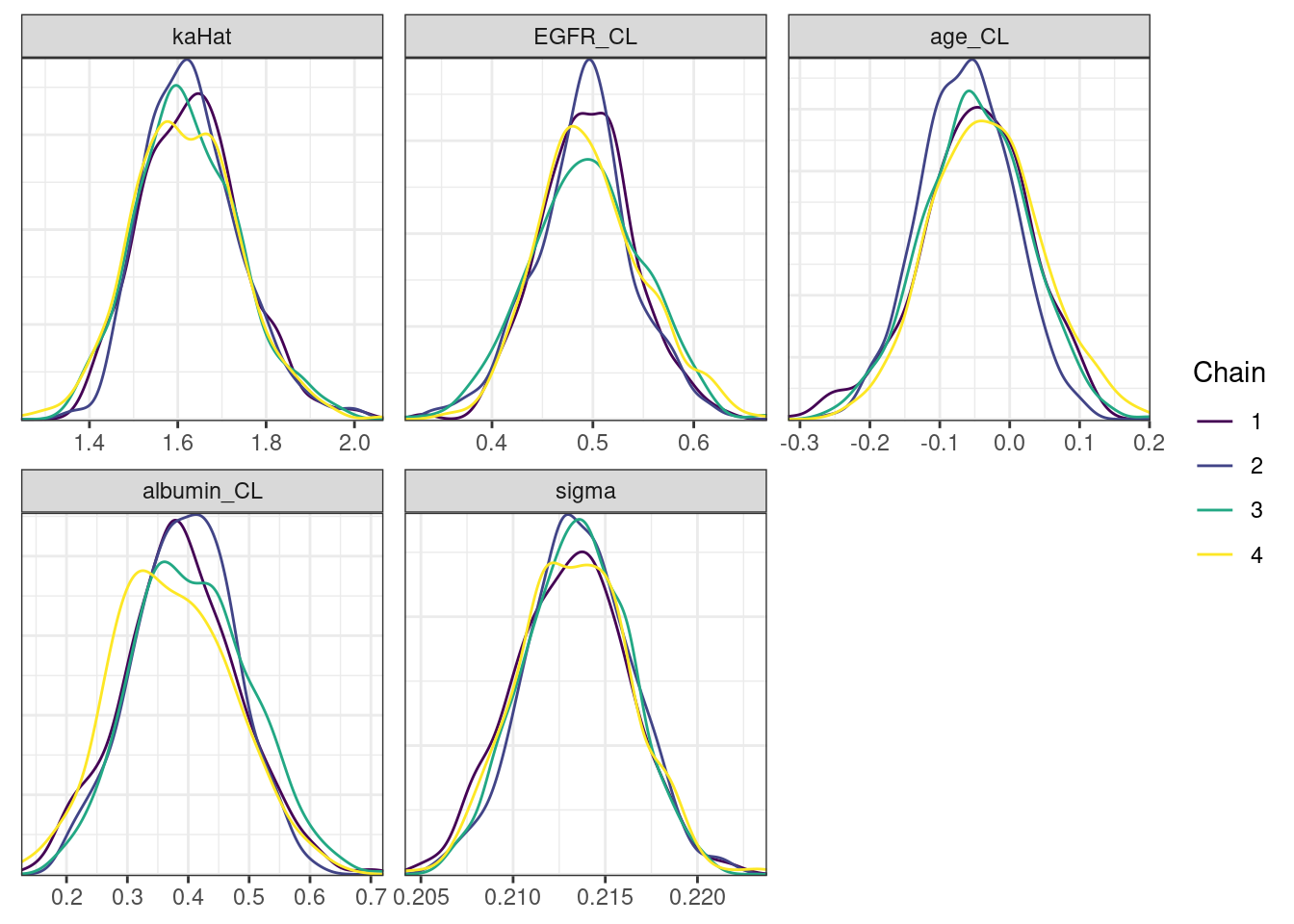
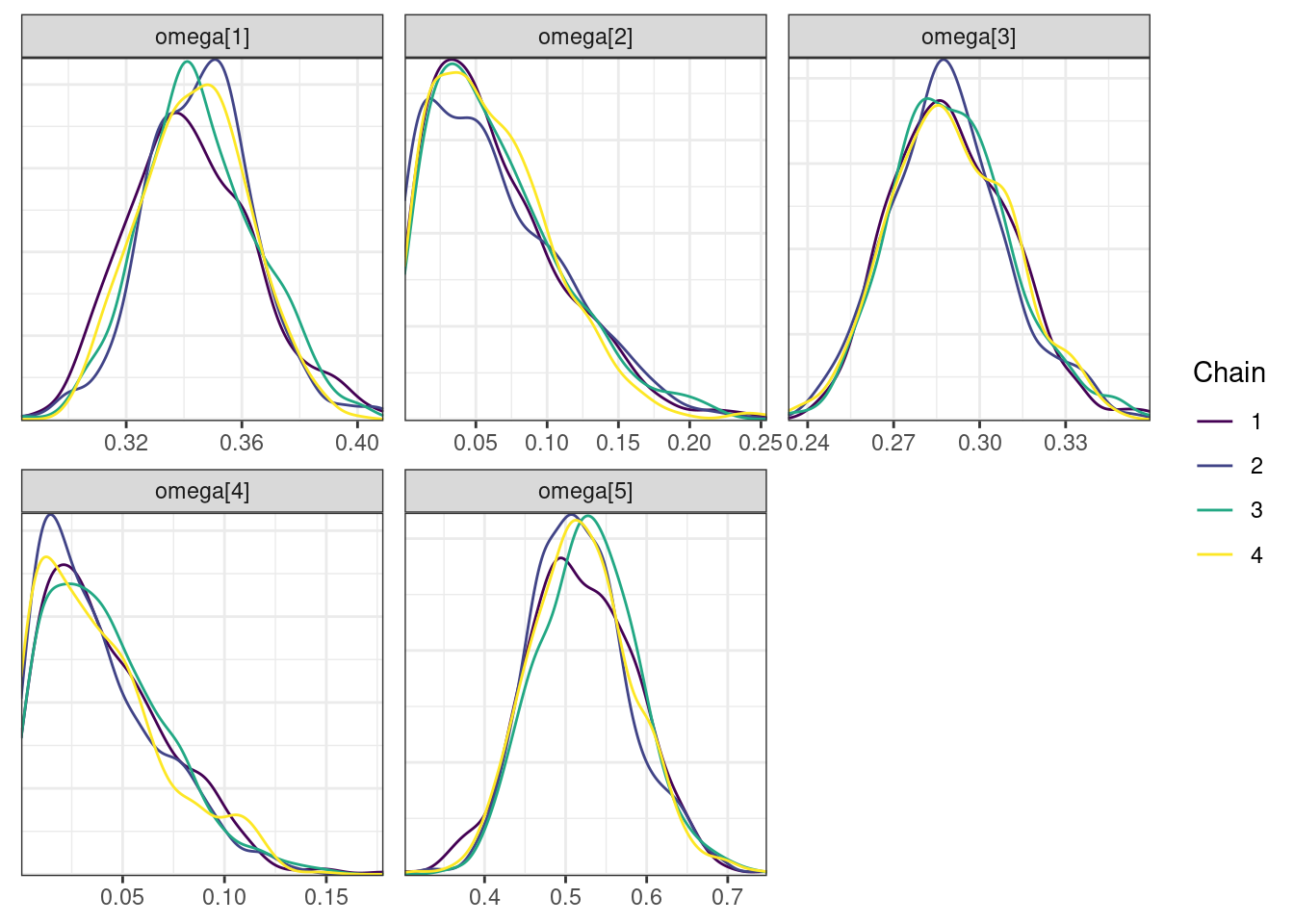
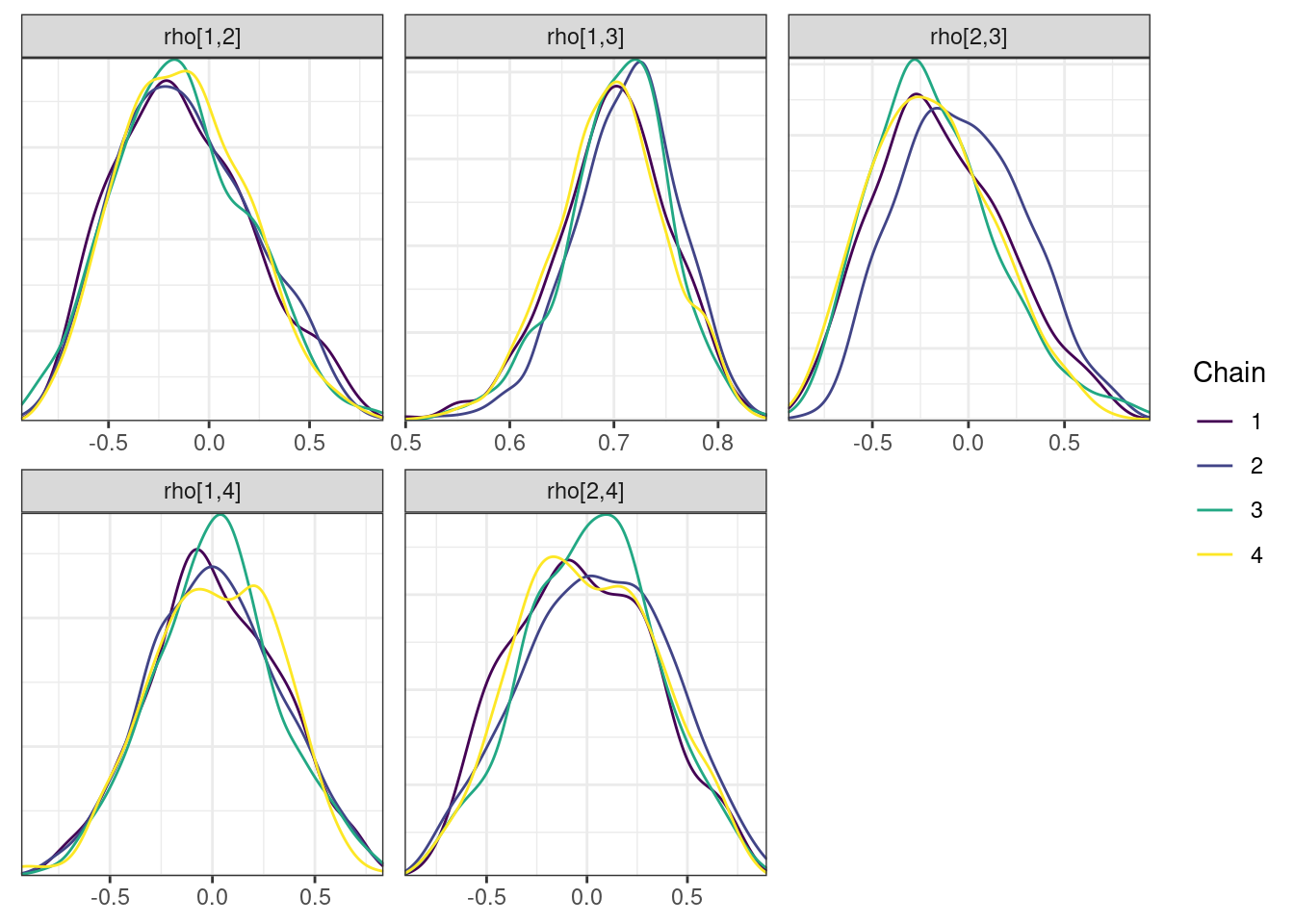
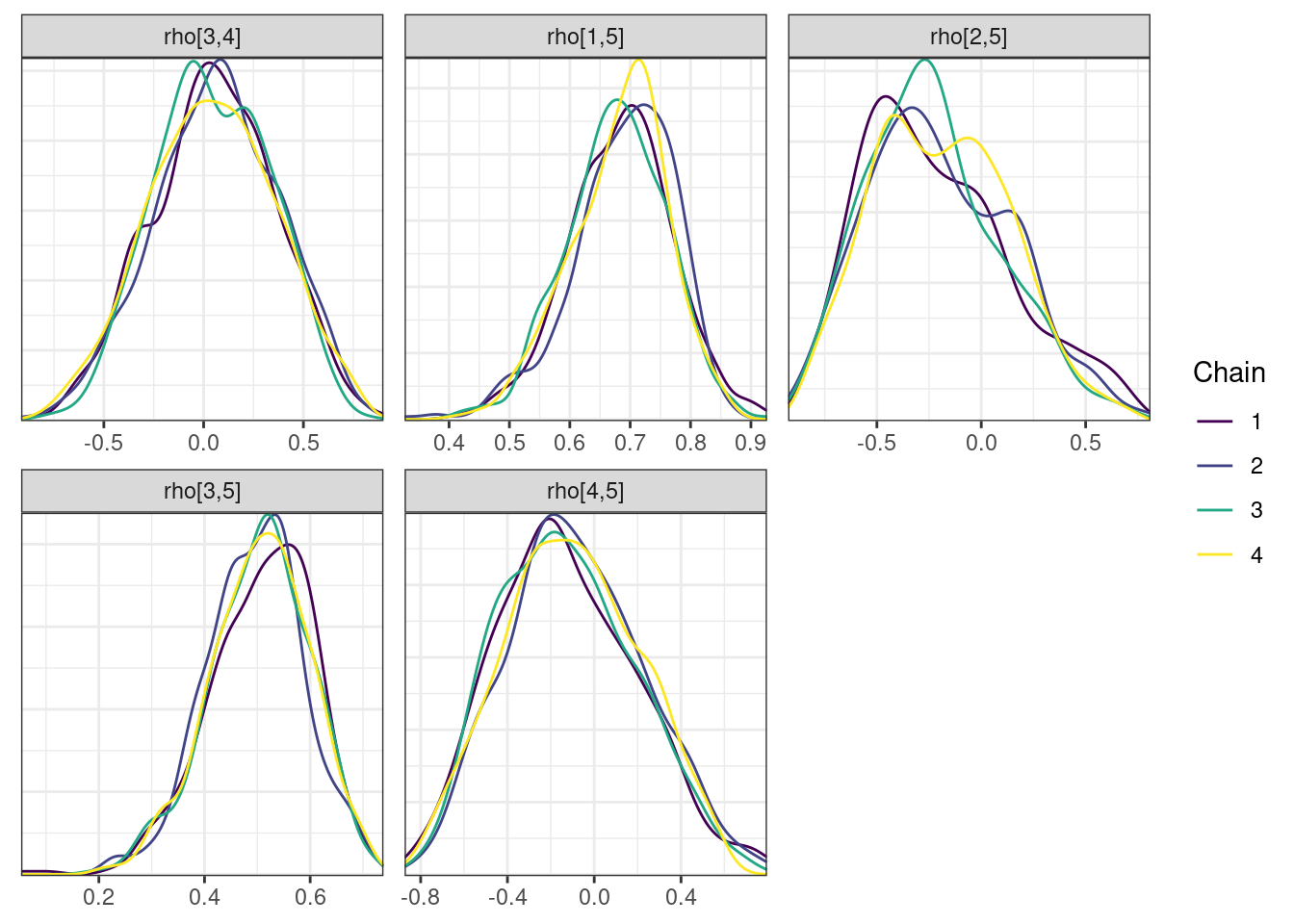
Figure 22: MCMC density plots for model ppkexpo4.

Figure 23: MCMC density plots for model ppkexpo4.

Figure 24: MCMC density plots for model ppkexpo4.

Figure 25: MCMC density plots for model ppkexpo4.

Figure 26: MCMC density plots for model ppkexpo4.

The overall log probability (lp__) has decreased relatively to ppkexpo3, suggesting some improvement in the model fit. As noted before, we discuss better metrics in a subsequent section. The sampling performance in this model is also more refined than in ppkexpo3.

Model evaluation

Let’s assess the ppkexpo4 model fit using posterior predictive checking.

load(file = here::here(dirname(get_data_path(mod)), "data1.RData"))
loq <- 10

data2 <- data1 %>%
  mutate(DV = if_else(EVID == 1, NA_real_, DV),
         DV = if_else(BLQ == 1, NA_real_, DV))

pred2 <- spread_draws(fit, 
                     cPredNew[num]) %>%
  mutate(cPredNew = ifelse(cPredNew < loq, NA_real_, cPredNew)) %>%
  left_join(data2 %>% mutate(num = 1:n())) %>%
  mutate(cPredNew = ifelse(EVID == 1 | TIME == 0, NA_real_, cPredNew))

ppc_all <- observed(data2, x = TIME, y = DV) %>%
  simulated(pred2 %>% arrange(.draw, num), y = cPredNew) %>% 
  stratify(~ STUDY) %>% 
  binning(bin = 'jenks', nbins = 10) %>% 
  vpcstats()
plot(ppc_all, legend.position = "top", 
     color = c("steelblue3", "grey60", "steelblue3"),
     linetype = c("dashed", "solid", "dashed"),
     ribbon.alpha = 0.5) + 
  scale_y_log10() +
  labs(x = "time (h)",
       y = "plasma drug concentration (mg/L)")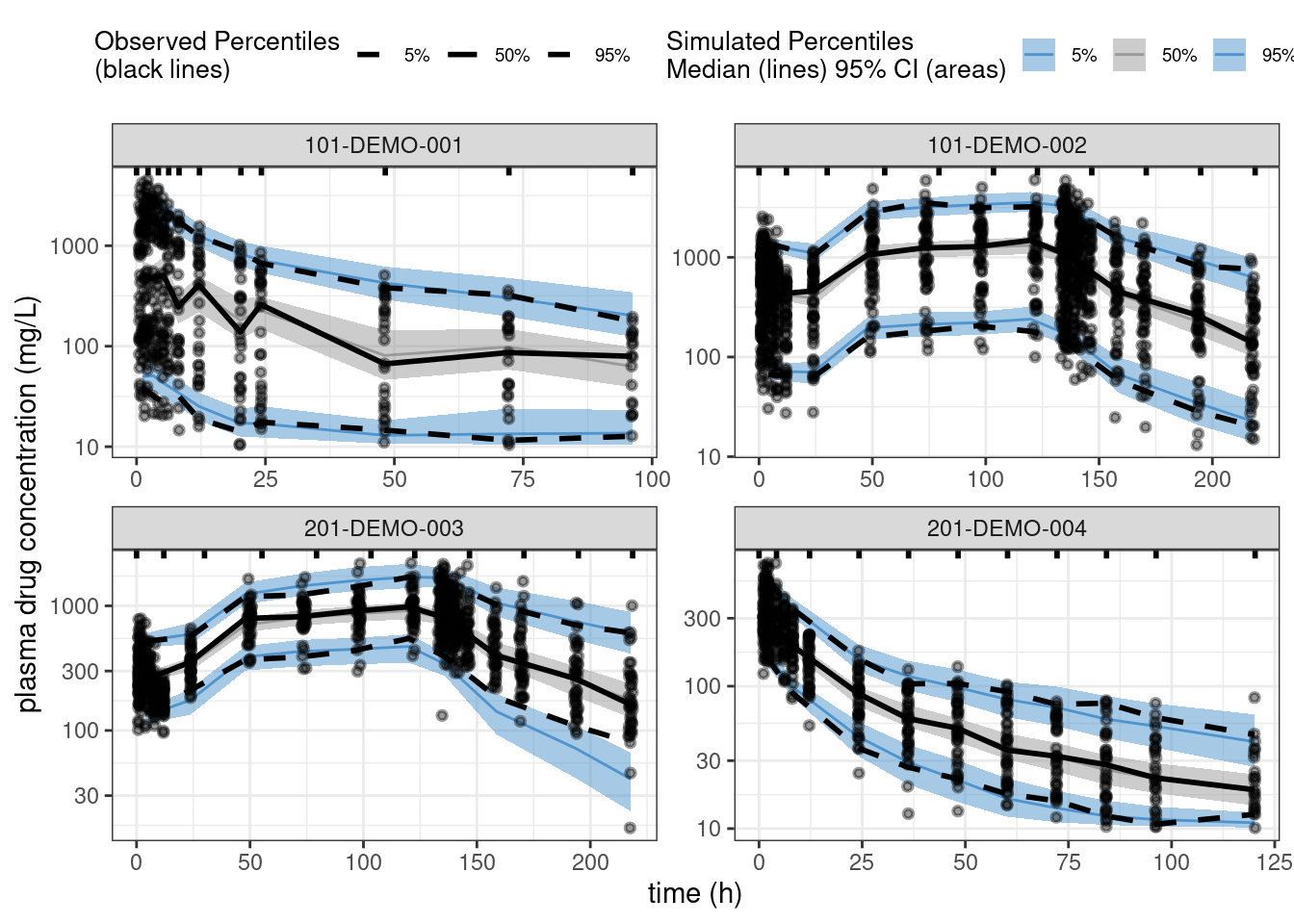

Figure 27: Posterior predictive check for model ppkexpo4.

PPCs for fraction of BLQs

This is a predictive check of the fraction of observations that are below the limit of quantification (BLQ) versus time. We take the single dose studies and limit the analysis out to 100 hours after the dose.

pred3 <- spread_draws(fit, 
                     cPredNew[num]) %>%
  left_join(data2 %>% mutate(num = 1:n())) %>%
  mutate(BLQsim = ifelse(cPredNew < loq, 1, 0),
         BLQsim = ifelse(EVID == 0, BLQsim, NA_integer_)) %>% 
  filter(STUDY %in% c("101-DEMO-001", "201-DEMO-004"),
         TIME <= 100)

data3 <- data2 %>%
  filter(STUDY %in% c("101-DEMO-001", "201-DEMO-004"),
         TIME <= 100)

ppc_blq <- observed(data3, x = TIME, y = BLQ) %>%
  simulated(pred3 %>% arrange(.draw, num), y = BLQsim) %>% 
  stratify(~ STUDY) %>% 
  binning(bin = 'jenks', nbins = 10) %>% 
  vpcstats(vpc.type = "categorical")

## Change factor labels to make more readable
ppc_blq$stats <- ppc_blq$stats %>%
  mutate(pname = factor(pname, labels = c(">= LOQ", "< LOQ")))
plot(ppc_blq, legend.position = "top",
     ribbon.alpha = 0.5,
     xlab = "time (h)",
     ylab = "fraction above or below LOQ")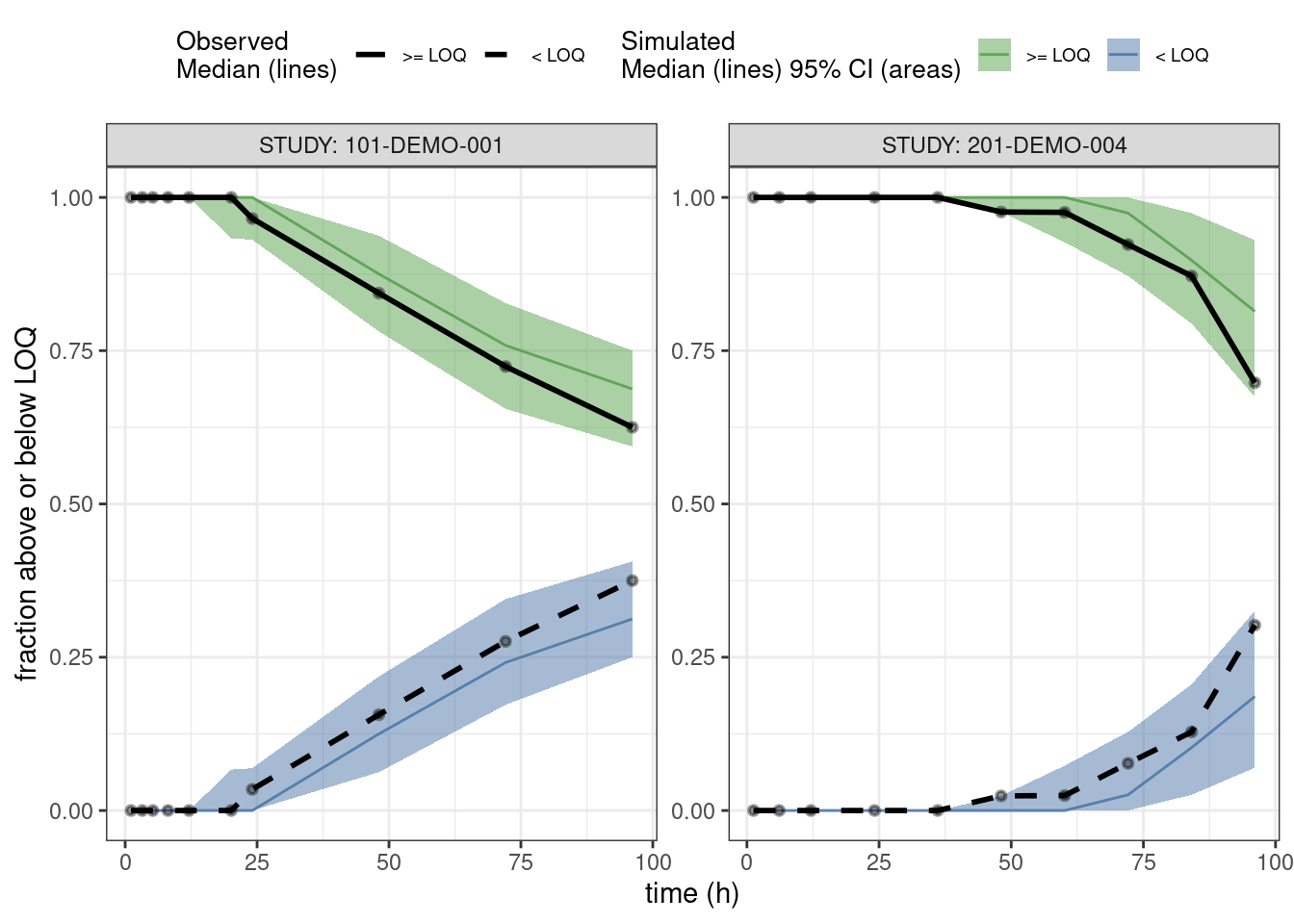

Figure 28: Posterior predictive check of the the fraction of observations that are BLQ for model ppkexpo4.

Other resources

The following script from the GitHub repository is discussed on this page. If you’re interested running this code, visit the About the GitHub Repo page first.

Update Model script: update-model.Rmd