Generated Quantities Models

Generated quantities model workflow with bbr.bayes.

bbr
bbr.bayes
model management
simulation

Introduction

We often want to perform further calculations using the posterior samples from previous model fits. Examples of such calculations include the following:

  • Generate additional posterior predictive checks or other model diagnostics that you didn’t anticipate when fitting the model.
  • Simulate patient outcomes for alternative treatment regimens or specific patient populations.
  • Simulate trial outcomes for potential future trial designs.

Such calculations can often be done most efficiently using cmdstan’s generated_quantities method, and bbr.bayes can provide convenient functions for implementing calculations using generated_quantities.

This section demonstrates the use of bbr.bayes generated_quantities functionality for calculations required for posterior predictive checks and for simulations of drug concentrations as a function of renal function (eGFR). Another application of generated_quantities is demonstrated in the “Summarizing and comparing models” section where we use this method to calculate metrics for model comparison.

For more information about the generate_quantities method, see the sections describing stand-alone generated quantities models in the quick-start portion of the Stand-alone Generated Quantities section of the CmdStan User’s Guide and the Generated Quantities section of the Stan User’s Guide.

Tools used

MetrumRG packages

bbr Manage, track, and report modeling activities, through simple R objects, with a user-friendly interface between R and NONMEM®.

bbr.bayes Extension of the bbr package to support Bayesian modeling with Stan or NONMEM®.

CRAN packages

dplyr A grammar of data manipulation.

bayesplot Plotting Bayesian models and diagnostics with ggplot.

posterior Provides tools for working with output from Bayesian models, including output from CmdStan.

tidyvpc Create visual predictive checks using tidyverse-style syntax.

tidybayes Integrate Bayesian modeling with the tidyverse.

Set up

Load required packages and set file paths to your model and figure directories.

library(bbr)
library(bbr.bayes)
library(here)
library(tidyverse)
library(yspec)
library(cmdstanr)
library(posterior)
library(bayesplot)
library(tidybayes)
library(tidyvpc)
library(glue)
library(kableExtra)

set_cmdstan_path(path = here("Torsten", "v0.91.0", "cmdstan"))

MODEL_DIR <- here("model", "stan")
FIGURE_DIR <- here("deliv", "figure")

Separating the model fitting and posterior predictive simulation tasks

The models presented so far (ppkexpo1 - ppkexpo4) include code in the generated quantities block to generate predicted values for use in posterior predictive checks. Thus, calculations for model fitting and posterior predictive checking is done in one step. Posterior predictions can contribute greatly to the size of the files containing the posterior samples, particularly, when analyzing large data sets. Additionally, the posterior predictive calculations contribute to the overall time required for computation. During more exploratory model development stages, you may want to postpone those posterior predictive calculations to speed up computation and reduce disk storage requirements. You can reserve the posterior predictive calculations for only the more promising model candidates without having to refit the model by exploiting cmdstan’s generated_quantities method.

Model creation and submission

Let’s start by replicating model ppkexpo4 without any content in the generated quantities block. Call it ppkexpo5.

ppkexpo4 <- read_model(here(MODEL_DIR, "ppkexpo4"))

ppkexpo5 <- copy_model_from(ppkexpo4, "ppkexpo5", .inherit_tags = TRUE, 
                      .overwrite = TRUE) %>%
  add_description("PopPK model: ppkexpo4 without simulations for PPCs")

Now, manually edit ppkexpo5.stan by deleting statements in the generated quantities block used to calculate posterior predictions. For this demo, we copy previously created files from the demo folder.

ppkexpo5 <- ppkexpo5 %>%
  add_stanmod_file(here(MODEL_DIR, "demo", "ppkexpo5.stan"))

Here is the resulting Stan model.

. /*
. Final PPK model
.   - Linear 2 compartment
.   - Non-centered parameterization
.   - lognormal residual variation
.   - Allometric scaling
.   - Additional covariates: EGFR, age, albumin
.   
. Based on NONMEM PopPK FOCE example project
. */
. 
. data{
.   int<lower = 1> nId; // number of individuals
.   int<lower = 1> nt; // number of events (rows in data set)
.   int<lower = 1> nObs; // number of PK observations
.   array[nObs] int<lower = 1> iObs; // event indices for PK observations
.   int<lower = 1> nBlq; // number of BLQ observations
.   array[nBlq] int<lower = 1> iBlq; // event indices for BLQ observations
.   array[nt] real<lower = 0> amt, time;
.   array[nt] int<lower = 1> cmt;
.   array[nt] int<lower = 0> evid;
.   array[nId] int<lower = 1> start, end; // indices of first & last observations
.   vector<lower = 0>[nId] weight, EGFR, age, albumin;
.   vector<lower = 0>[nObs] cObs;
.   real<lower = 0> LOQ;
. }
. 
. transformed data{
.   int<lower = 1> nRandom = 5, nCmt = 3;
.   array[nt] real<lower = 0> rate = rep_array(0.0, nt), 
.                             ii = rep_array(0.0, nt);
.   array[nt] int<lower = 0> addl = rep_array(0, nt), 
.                            ss = rep_array(0, nt);
.   array[nId, nCmt] real F = rep_array(1.0, nId, nCmt), 
.                         tLag = rep_array(0.0, nId, nCmt);
.   }
. 
. parameters{
.   real<lower = 0> CLHat, QHat, V2Hat, V3Hat;
. // To constrain kaHat > lambda1 uncomment the following
.   real<lower = (CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat +
.       sqrt((CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat)^2 -
.            4 * CLHat / V2Hat * QHat / V3Hat)) / 2> kaHat; // ka > lambda_1
.   real EGFR_CL, age_CL, albumin_CL;
.   
.   real<lower = 0> sigma;
.   vector<lower = 0>[nRandom] omega;
. //  corr_matrix[nRandom] rho;
. //  array[nId] vector[nRandom] theta;
.   cholesky_factor_corr[nRandom] L_corr;
.   matrix[nRandom, nId] z;
. }
. 
. transformed parameters{
.   vector[nRandom] thetaHat = log([CLHat, QHat, V2Hat, V3Hat, kaHat]');
.   // Individual parameters
.   matrix[nId, nRandom] theta = (rep_matrix(thetaHat, nId) + diag_pre_multiply(omega, L_corr * z))';
.   vector<lower = 0>[nId] CL = exp(theta[,1] + 0.75 * log(weight / 70) +
.                               EGFR_CL * log(EGFR / 90) +
.                               age_CL * log(age / 35) +
.                               albumin_CL * log(albumin / 4.5)),
.                          Q = exp(theta[,2] + 0.75 * log(weight / 70)),
.                          V2 = exp(theta[,3] + log(weight / 70)),
.                          V3 = exp(theta[,4] + log(weight / 70)),
.                          ka = exp(theta[,5]);
.   corr_matrix[nRandom] rho =  L_corr * L_corr';
. 
.   row_vector[nt] cHat; // predicted concentration
.   matrix[nCmt, nt] x; // mass in all compartments
.   
.   for(j in 1:nId){
.     x[, start[j]:end[j]] = pmx_solve_twocpt(time[start[j]:end[j]],
.                                             amt[start[j]:end[j]],
.                                             rate[start[j]:end[j]],
.                                             ii[start[j]:end[j]],
.                                             evid[start[j]:end[j]],
.                                             cmt[start[j]:end[j]],
.                                             addl[start[j]:end[j]],
.                                             ss[start[j]:end[j]],
.                                             {CL[j], Q[j], V2[j], V3[j], ka[j]});
. 
.     cHat[start[j]:end[j]] = x[2, start[j]:end[j]] / V2[j];
.   }
. }
. 
. model{
.   // priors
.   CLHat ~ normal(0, 10); 
.   QHat ~ normal(0, 10);
.   V2Hat ~ normal(0, 50);
.   V3Hat ~ normal(0, 100);
.   kaHat ~ normal(0, 3);
.   EGFR_CL ~ normal(0, 2);
.   age_CL ~ normal(0, 2);
.   albumin_CL ~ normal(0, 2);
.   
.   sigma ~ normal(0, 0.5);
.   omega ~ normal(0, 0.5); 
.   L_corr ~ lkj_corr_cholesky(2);
.   
.   // interindividual variability
.   to_vector(z) ~ normal(0, 1);
. 
.   // likelihood
.   cObs ~ lognormal(log(cHat[iObs]), sigma); // observed data likelihood
.   target += lognormal_lcdf(LOQ | log(cHat[iBlq]), sigma); // BLQ data likelihood
. 
. }
. 
. generated quantities{
. 
. }

ppkexpo5: Submit the model

## Set cmdstanr arguments
ppkexpo5 <- ppkexpo5 %>%
  set_stanargs(list(iter_warmup = 500,
                    iter_sampling = 500,
                    thin = 1,
                    chains = 4,
                    parallel_chains = 4,
##                    refresh = 10,
                    seed = 1234,
                    save_warmup = FALSE),
               .clear = TRUE)

## Check that the necessary files are present
check_stan_model(ppkexpo4)

## Fit the model using Stan
ppkexpo5_fit <- ppkexpo5 %>% submit_model(.overwrite = TRUE)

ppkexpo5: Parameter summary and sampling diagnostics

model_name <- "ppkexpo5"
mod <- read_model(here(MODEL_DIR, model_name))
fit <- read_fit_model(mod)

fit$cmdstan_diagnose()
. Processing csv files: /data/expo4-torsten-poppk/model/stan/ppkexpo5/ppkexpo5-output/ppkexpo5-202409280745-1-69fdb2.csv, /data/expo4-torsten-poppk/model/stan/ppkexpo5/ppkexpo5-output/ppkexpo5-202409280745-2-69fdb2.csv, /data/expo4-torsten-poppk/model/stan/ppkexpo5/ppkexpo5-output/ppkexpo5-202409280745-3-69fdb2.csv, /data/expo4-torsten-poppk/model/stan/ppkexpo5/ppkexpo5-output/ppkexpo5-202409280745-4-69fdb2.csv
. 
. Checking sampler transitions treedepth.
. Treedepth satisfactory for all transitions.
. 
. Checking sampler transitions for divergences.
. No divergent transitions found.
. 
. Checking E-BFMI - sampler transitions HMC potential energy.
. E-BFMI satisfactory.
. 
. Effective sample size satisfactory.
. 
. The following parameters had split R-hat greater than 1.05:
.   L_corr[3,2]
. Such high values indicate incomplete mixing and biased estimation.
. You should consider regularizating your model with additional prior information or a more effective parameterization.
. 
. Processing complete.
pars <- c("lp__", "CLHat", "QHat", "V2Hat", "V3Hat", "kaHat",
          "EGFR_CL", "age_CL", "albumin_CL",
          "sigma", glue("omega[{1:5}]"),
          paste0("rho[", matrix(apply(expand.grid(1:5, 1:5),
                                      1, paste, collapse = ","),
                                ncol = 5)[upper.tri(diag(5), 
                                                    diag = FALSE)], "]"))
# Get posterior samples for parameters of interest
posterior <- fit$draws(variables = pars)
# Get quantities related to NUTS performance, e.g., occurrence of
# divergent transitions
np <- nuts_params(fit) 

n_iter <- dim(posterior)[1]
n_chains <- dim(posterior)[2]

ptable <- fit$summary(variables = pars) %>%
  mutate(across(-variable, ~ pmtables::sig(.x, maxex = 4))) %>% 
  rename(parameter = variable) %>%
  mutate("90% CI" = paste("(", q5, ", ", q95, ")", 
                          sep = "")) %>%
  select(parameter, mean, median, sd, mad, "90% CI", ess_bulk, ess_tail, rhat)

ptable %>% 
  kable %>%
  kable_styling()
parameter mean median sd mad 90% CI ess_bulk ess_tail rhat
lp__ -31.1 -30.4 27.1 26.7 (-76.9, 13.5) 429 630 1.01
CLHat 3.28 3.27 0.0928 0.0915 (3.13, 3.43) 168 254 1.02
QHat 3.76 3.75 0.159 0.159 (3.50, 4.02) 932 1120 1.00
V2Hat 61.6 61.7 1.79 1.78 (58.8, 64.6) 396 709 1.01
V3Hat 67.7 67.7 1.51 1.45 (65.2, 70.2) 2250 1740 1.00
kaHat 1.63 1.62 0.113 0.112 (1.45, 1.82) 709 1170 1.00
EGFR_CL 0.492 0.492 0.0472 0.0462 (0.414, 0.569) 515 974 1.01
age_CL -0.0429 -0.0415 0.0759 0.0740 (-0.172, 0.0848) 355 483 1.02
albumin_CL 0.391 0.391 0.0910 0.0937 (0.246, 0.541) 438 765 1.01
sigma 0.213 0.213 0.00289 0.00285 (0.209, 0.218) 3110 1530 1.00
omega[1] 0.342 0.342 0.0193 0.0188 (0.311, 0.374) 302 600 1.00
omega[2] 0.0631 0.0559 0.0457 0.0470 (0.00441, 0.146) 691 1050 1.00
omega[3] 0.290 0.289 0.0209 0.0205 (0.257, 0.327) 657 1280 1.01
omega[4] 0.0418 0.0361 0.0299 0.0310 (0.00396, 0.0967) 712 1220 1.00
omega[5] 0.520 0.518 0.0616 0.0625 (0.421, 0.625) 777 1230 1.00
rho[1,2] -0.141 -0.165 0.321 0.323 (-0.640, 0.441) 2690 1290 1.00
rho[1,3] 0.704 0.707 0.0527 0.0542 (0.614, 0.784) 509 1090 1.00
rho[2,3] -0.136 -0.161 0.336 0.353 (-0.639, 0.462) 85.2 133 1.03
rho[1,4] 0.0176 0.0150 0.299 0.306 (-0.480, 0.510) 3750 1450 1.00
rho[2,4] 0.0152 0.0190 0.356 0.390 (-0.570, 0.590) 2000 1630 1.00
rho[3,4] 0.0463 0.0403 0.305 0.317 (-0.447, 0.543) 4160 1390 1.00
rho[1,5] 0.684 0.689 0.0787 0.0775 (0.549, 0.804) 969 1320 1.00
rho[2,5] -0.217 -0.246 0.338 0.346 (-0.707, 0.412) 401 654 1.01
rho[3,5] 0.504 0.513 0.0930 0.0891 (0.347, 0.647) 1220 1540 1.00
rho[4,5] -0.0902 -0.104 0.320 0.332 (-0.594, 0.460) 363 932 1.01

As expected, the results are essentially the same as those for ppkexpo4. Suppose we want to perform posterior predictive checking since he samples generated by the ppkexpo5 fitting did not include the posterior predictions we needed. We do that as a separate step.

Model ppkexpo5_gq1: Simulations for PPCs

To construct our generated quantities model, we copy the ppkexpo5 model using a specialized copy_model_from function called copy_model_as_stan_gq. In addition to copying the files from the ppkexpo5 model like copy_model_from does, copy_model_as_stan_gq generates a ppkexpo5-fitted-param.R file that contains a function for getting the posterior samples from the parent model.

ppkexpo5 <- read_model(here(MODEL_DIR, "ppkexpo5"))

ppkexpo5_gq1 <- copy_model_as_stan_gq(ppkexpo5, "ppkexpo5_gq1", .inherit_tags = TRUE, 
                      .overwrite = TRUE) %>%
  add_description("PopPK model: ppkexpo5 model to generate simulations for PPCs")

Now, manually edit ppkexpo5_gq1.stan by deleting the contents of the model block and adding simulation code in the generated quantities block. For this demo, we copy previously created files from the demo folder.

ppkexpo5_gq1 <- ppkexpo5_gq1 %>%
  add_stanmod_file(here(MODEL_DIR, "demo", "ppkexpo5_gq1.stan"))

Here is the resulting Stan model.

. /*
. Generate simulations for PPCs using final PPK model
.   - Linear 2 compartment
.   - Non-centered parameterization
.   - lognormal residual variation
.   - Allometric scaling
.   - Additional covariates: EGFR, age, albumin
.   
. Based on NONMEM PopPK FOCE example project
. */
. 
. data{
.   int<lower = 1> nId; // number of individuals
.   int<lower = 1> nt; // number of events (rows in data set)
.   int<lower = 1> nObs; // number of PK observations
.   array[nObs] int<lower = 1> iObs; // event indices for PK observations
.   int<lower = 1> nBlq; // number of BLQ observations
.   array[nBlq] int<lower = 1> iBlq; // event indices for BLQ observations
.   array[nt] real<lower = 0> amt, time;
.   array[nt] int<lower = 1> cmt;
.   array[nt] int<lower = 0> evid;
.   array[nId] int<lower = 1> start, end; // indices of first & last observations
.   vector<lower = 0>[nId] weight, EGFR, age, albumin;
.   vector<lower = 0>[nObs] cObs;
.   real<lower = 0> LOQ;
. }
. 
. transformed data{
.   int<lower = 1> nRandom = 5, nCmt = 3;
.   array[nt] real<lower = 0> rate = rep_array(0.0, nt), 
.                             ii = rep_array(0.0, nt);
.   array[nt] int<lower = 0> addl = rep_array(0, nt), 
.                            ss = rep_array(0, nt);
.   array[nId, nCmt] real F = rep_array(1.0, nId, nCmt), 
.                         tLag = rep_array(0.0, nId, nCmt);
.   }
. 
. parameters{
.   real<lower = 0> CLHat, QHat, V2Hat, V3Hat;
. // To constrain kaHat > lambda1 uncomment the following
.   real<lower = (CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat +
.       sqrt((CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat)^2 -
.            4 * CLHat / V2Hat * QHat / V3Hat)) / 2> kaHat; // ka > lambda_1
.   real EGFR_CL, age_CL, albumin_CL;
.   
.   real<lower = 0> sigma;
.   vector<lower = 0>[nRandom] omega;
. //  corr_matrix[nRandom] rho;
. //  array[nId] vector[nRandom] theta;
.   cholesky_factor_corr[nRandom] L_corr;
.   matrix[nRandom, nId] z;
. }
. 
. transformed parameters{
.   vector[nRandom] thetaHat = log([CLHat, QHat, V2Hat, V3Hat, kaHat]');
.   // Individual parameters
.   matrix[nId, nRandom] theta = (rep_matrix(thetaHat, nId) + diag_pre_multiply(omega, L_corr * z))';
.   vector<lower = 0>[nId] CL = exp(theta[,1] + 0.75 * log(weight / 70) +
.                               EGFR_CL * log(EGFR / 90) +
.                               age_CL * log(age / 35) +
.                               albumin_CL * log(albumin / 4.5)),
.                          Q = exp(theta[,2] + 0.75 * log(weight / 70)),
.                          V2 = exp(theta[,3] + log(weight / 70)),
.                          V3 = exp(theta[,4] + log(weight / 70)),
.                          ka = exp(theta[,5]);
.   corr_matrix[nRandom] rho =  L_corr * L_corr';
. 
.   row_vector[nt] cHat; // predicted concentration
.   matrix[nCmt, nt] x; // mass in all compartments
.   
.   for(j in 1:nId){
.     x[, start[j]:end[j]] = pmx_solve_twocpt(time[start[j]:end[j]],
.                                             amt[start[j]:end[j]],
.                                             rate[start[j]:end[j]],
.                                             ii[start[j]:end[j]],
.                                             evid[start[j]:end[j]],
.                                             cmt[start[j]:end[j]],
.                                             addl[start[j]:end[j]],
.                                             ss[start[j]:end[j]],
.                                             {CL[j], Q[j], V2[j], V3[j], ka[j]});
. 
.     cHat[start[j]:end[j]] = x[2, start[j]:end[j]] / V2[j];
.   }
. }
. 
. model{
. 
. }
. 
. generated quantities{
.   // Individual parameters for hypothetical new individuals
.   matrix[nRandom, nId] zNew;
.   matrix[nId, nRandom] thetaNew;
.   vector<lower = 0>[nId] CLNew, QNew, V2New, V3New, kaNew;
. 
.   row_vector[nt] cHatNew; // predicted concentration in new individuals
.   matrix[nCmt, nt] xNew; // mass in all compartments in new individuals
.   array[nt] real cPred, cPredNew;
. 
.   vector[nObs + nBlq] log_lik;
. 
.   // Simulations for posterior predictive checks
.   for(j in 1:nId){
.     zNew[,j] = to_vector(normal_rng(rep_vector(0, nRandom), 1));
.   }
.   thetaNew = (rep_matrix(thetaHat, nId) + diag_pre_multiply(omega, L_corr * zNew))';
.   CLNew = exp(thetaNew[,1] + 0.75 * log(weight / 70) +
.           EGFR_CL * log(EGFR / 90) +
.           age_CL * log(age / 35) +
.           albumin_CL * log(albumin / 4.5));
.   QNew = exp(thetaNew[,2] + 0.75 * log(weight / 70));
.   V2New = exp(thetaNew[,3] + log(weight / 70));
.   V3New = exp(thetaNew[,4] + log(weight / 70));
.   kaNew = exp(thetaNew[,5]);
. 
.   for(j in 1:nId){
.     xNew[, start[j]:end[j]] = pmx_solve_twocpt(time[start[j]:end[j]],
.                                                amt[start[j]:end[j]],
.                                                rate[start[j]:end[j]],
.                                                ii[start[j]:end[j]],
.                                                evid[start[j]:end[j]],
.                                                cmt[start[j]:end[j]],
.                                                addl[start[j]:end[j]],
.                                                ss[start[j]:end[j]],
.                                                {CLNew[j], QNew[j], V2New[j], 
.                                                V3New[j], kaNew[j]});
. 
.     cHatNew[start[j]:end[j]] = xNew[2, start[j]:end[j]] / V2New[j];
. 
.     
.     cPred[start[j]] = 0.0;
.     cPredNew[start[j]] = 0.0;
.     // new observations in existing individuals
.     cPred[(start[j] + 1):end[j]] = lognormal_rng(log(cHat[(start[j] + 1):end[j]]), 
.       sigma);
.     // new observations in new individuals
.     cPredNew[(start[j] + 1):end[j]] = lognormal_rng(log(cHatNew[(start[j] + 1):end[j]]), 
.       sigma); 
.   }
.   
.   // Calculate log-likelihood values to use for LOO CV
.   
.   // Observation-level log-likelihood
.   for(i in 1:nObs)
.     log_lik[i] = lognormal_lpdf(cObs[i] | log(cHat[iObs[i]]), sigma);
.   for(i in 1:nBlq)
.     log_lik[i + nObs] = lognormal_lcdf(LOQ | log(cHat[iBlq[i]]), sigma);
. 
. }

ppkexpo5_gq1: Submit the model

## Set cmdstanr arguments
ppkexpo5_gq1 <- ppkexpo5_gq1 %>%
  set_stanargs(list(parallel_chains = 4,
                    seed = 1234),
               .clear = TRUE)

## Check that the necessary files are present
check_stan_model(ppkexpo5_gq1)

## Simulate using Stan
ppkexpo5_gq1_sim <- ppkexpo5_gq1 %>% submit_model(.overwrite = TRUE)

Model evaluation

We can now construct posterior predictive checks using the predicted values generated with ppkexpo5_gq1.

model_name <- "ppkexpo5_gq1"
mod <- read_model(here(MODEL_DIR, model_name))
fit <- read_fit_model(mod)

load(file = here::here(dirname(get_data_path(mod)), "data1.RData"))
loq <- 10

data2 <- data1 %>%
  mutate(DV = if_else(EVID == 1, NA_real_, DV),
         DV = if_else(BLQ == 1, NA_real_, DV))

pred2 <- spread_draws(fit, 
                     cPredNew[num]) %>%
  mutate(cPredNew = ifelse(cPredNew < loq, NA_real_, cPredNew)) %>%
  left_join(data2 %>% mutate(num = 1:n())) %>%
  mutate(cPredNew = ifelse(EVID == 1 | TIME == 0, NA_real_, cPredNew))

ppc_all <- observed(data2, x = TIME, y = DV) %>%
  simulated(pred2 %>% arrange(.draw, num), y = cPredNew) %>% 
  stratify(~ STUDY) %>% 
  binning(bin = 'jenks', nbins = 10) %>% 
  vpcstats()
plot(ppc_all, legend.position = "top", 
     color = c("steelblue3", "grey60", "steelblue3"),
     linetype = c("dashed", "solid", "dashed"),
     ribbon.alpha = 0.5) + 
  scale_y_log10() +
  labs(x = "time (h)",
       y = "plasma drug concentration (mg/L)")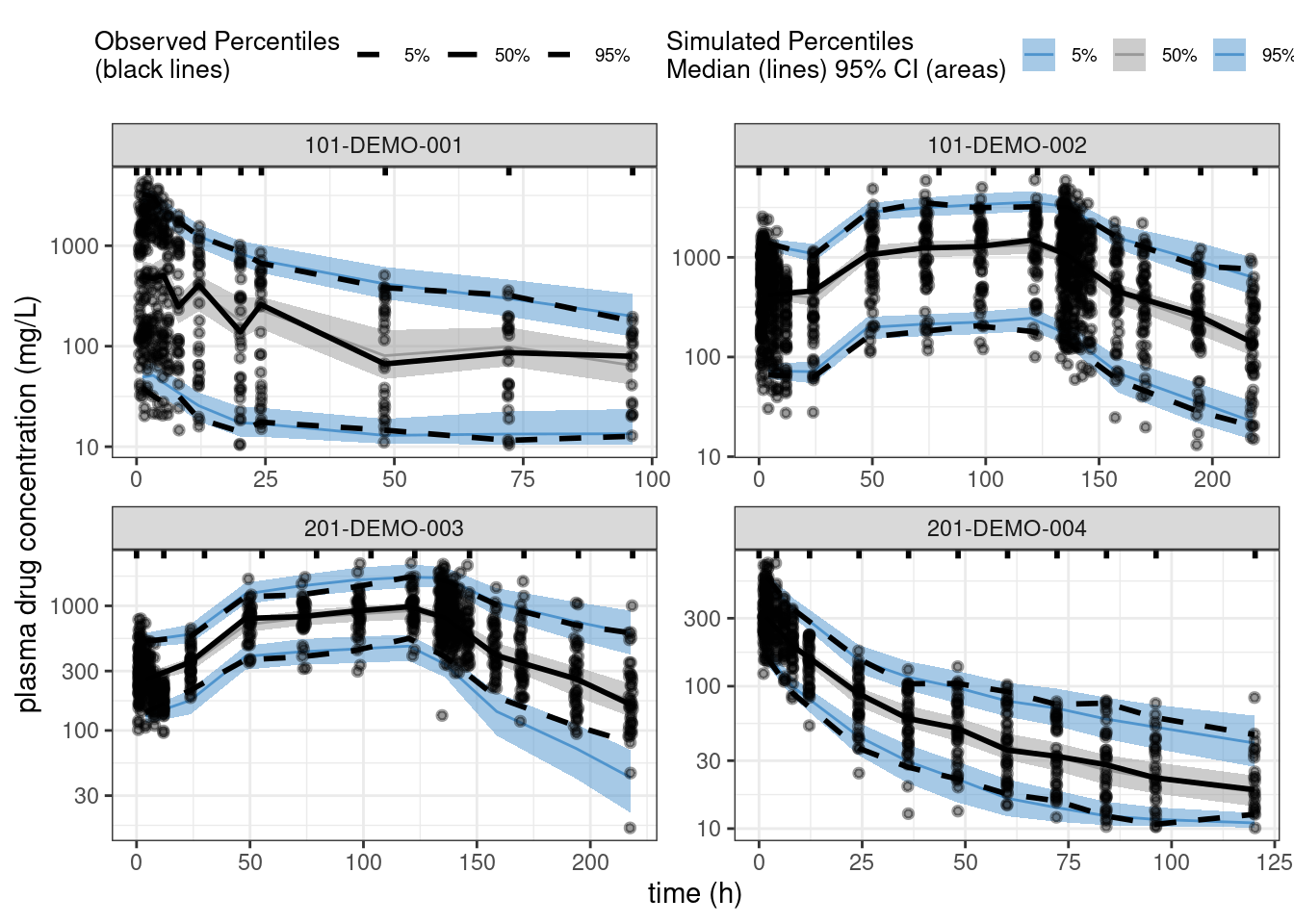

Figure 1: Posterior predictive check for model ppkexpo4.

PPCs for fraction of BLQs

This is a predictive check on the fraction of observations below limit of quantification (BLQ) versus time. We take just the single dose studies and limit the analysis out to 100 hours after the dose.

pred3 <- spread_draws(fit, 
                     cPredNew[num]) %>%
  left_join(data2 %>% mutate(num = 1:n())) %>%
  mutate(BLQsim = ifelse(cPredNew < loq, 1, 0),
         BLQsim = ifelse(EVID == 0, BLQsim, NA_integer_)) %>% 
  filter(STUDY %in% c("101-DEMO-001", "201-DEMO-004"),
         TIME <= 100)

data3 <- data2 %>%
  filter(STUDY %in% c("101-DEMO-001", "201-DEMO-004"),
         TIME <= 100)

ppc_blq <- observed(data3, x = TIME, y = BLQ) %>%
  simulated(pred3 %>% arrange(.draw, num), y = BLQsim) %>% 
  stratify(~ STUDY) %>% 
  binning(bin = 'jenks', nbins = 10) %>% 
  vpcstats(vpc.type = "categorical")

## Change factor labels to make more readable
ppc_blq$stats <- ppc_blq$stats %>%
  mutate(pname = factor(pname, labels = c(">= LOQ", "< LOQ")))
plot(ppc_blq, legend.position = "top",
     ribbon.alpha = 0.5,
     xlab = "time (h)",
     ylab = "fraction above or below LOQ")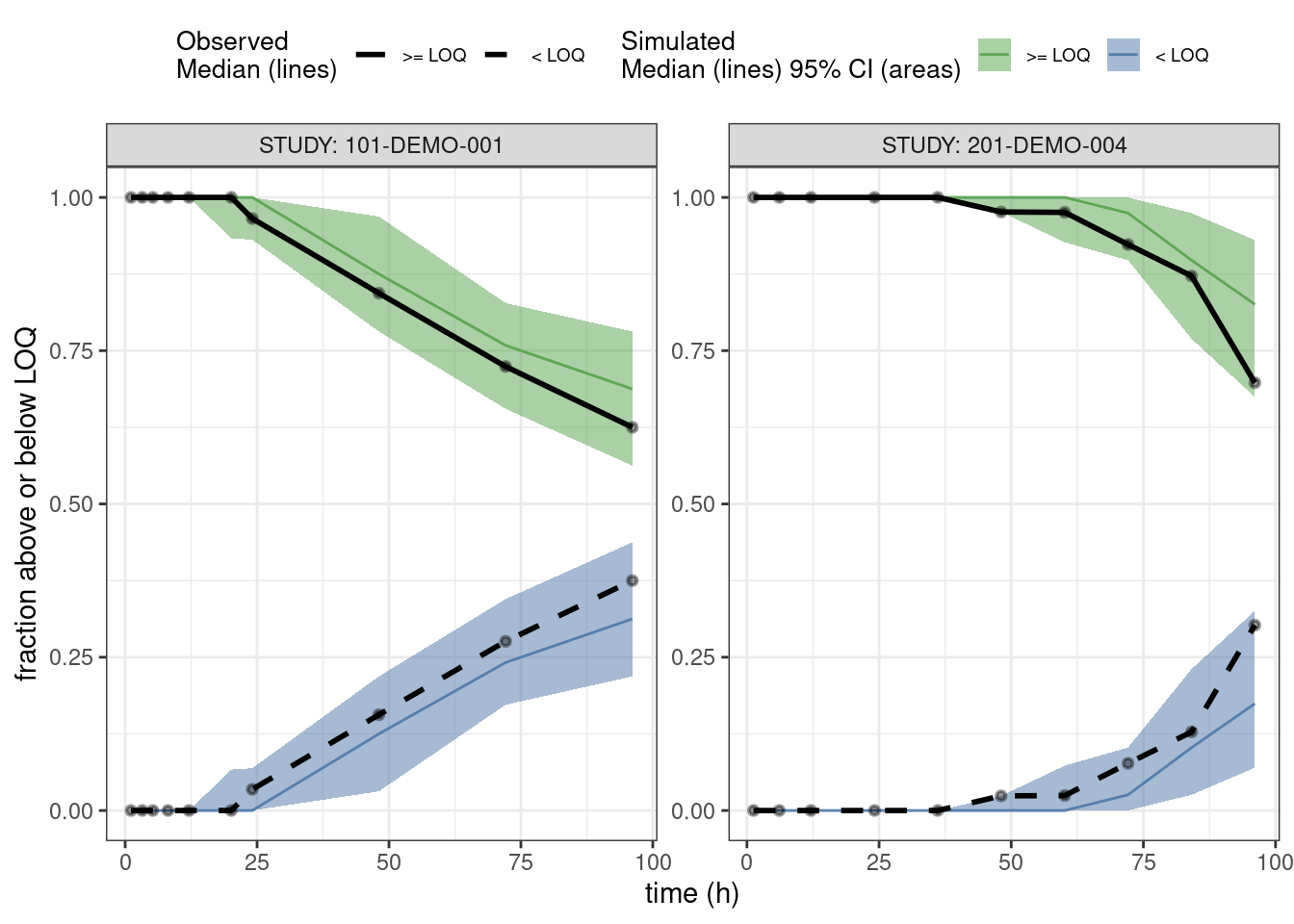

Figure 2: Posterior predictive check of the the fraction of observations that are BLQ for model ppkexpo4.

Simulation of the probable range of plasma concentrations as a function of eGFR

Let’s use a generated quantities model to simulate posterior-predicted plasma concentrations in “typical” patients with different eGFR measurements. We define a “typical” patient as a 35-year-old that weighs 70 kg and with an albumin of 4.5 g/dL.

The idea is to calculate posterior predictive intervals for the population median, 5th percentile, and 95th percentile of the plasma drug concentration as a function of time. We use Stan/Torsten to simulate outcomes for a large population of individual patients for each posterior sample and to calculate the relevant quantiles at each time. That way, we only need to save the summary statistics to a file rather than all of the individual patient values.

ppkexpo5 <- read_model(here(MODEL_DIR, "ppkexpo5"))

ppkexpo5_gq2 <- copy_model_as_stan_gq(ppkexpo5, "ppkexpo5_gq2", 
                                      .inherit_tags = TRUE, 
                                      .overwrite = TRUE) %>%
  add_description("PopPK model: ppkexpo5 model to simulate PK as a function of EGFR")

Now, manually edit ppkexpo5_gq2.stan by revising the generated quantities block.

Copy the previously created files from the demo folder.

ppkexpo5_gq2 <- ppkexpo5_gq2 %>%
  add_stanmod_file(here(MODEL_DIR, "demo", "ppkexpo5_gq2.stan"))

Here is the resulting Stan model.

. /*
. Generate simulations for patients with different EGFR levels
. using final PPK model
.   - Linear 2 compartment
.   - Non-centered parameterization
.   - lognormal residual variation
.   - Allometric scaling
.   - Additional covariates: EGFR, age, albumin
.   
. Based on NONMEM PopPK FOCE example project
. */
. 
. data{
.   int<lower = 1> nId; // number of individuals
.   int<lower = 1> nt; // number of events (rows in data set)
.   int<lower = 1> nObs; // number of PK observations
.   array[nObs] int<lower = 1> iObs; // event indices for PK observations
.   int<lower = 1> nBlq; // number of BLQ observations
.   array[nBlq] int<lower = 1> iBlq; // event indices for BLQ observations
.   array[nt] real<lower = 0> amt, time;
.   array[nt] int<lower = 1> cmt;
.   array[nt] int<lower = 0> evid;
.   array[nId] int<lower = 1> start, end; // indices of first & last observations
.   vector<lower = 0>[nId] weight, EGFR, age, albumin;
.   vector<lower = 0>[nObs] cObs;
.   real<lower = 0> LOQ;
. }
. 
. transformed data{
.   // Number of simulated individuals
.   int nIdSim = 1000;
.   
.   // Data structure for each individual
.   int ntSim = 193;
.   int<lower = 1> nRandom = 5, nCmt = 3;
.   array[ntSim] real<lower = 0> amtSim = rep_array(0.0, ntSim),
.                             timeSim;
.   array[ntSim] int<lower = 1> cmtSim = rep_array(1, ntSim);
.   array[ntSim] int<lower = 0> evidSim = rep_array(0, ntSim);
.   array[ntSim] real<lower = 0> rateSim = rep_array(0.0, ntSim), 
.                             iiSim = rep_array(0.0, ntSim);
.   array[ntSim] int<lower = 0> addlSim = rep_array(0, ntSim), 
.                            ssSim = rep_array(0, ntSim);
.   //array[nId, nCmt] real FSim = rep_array(1.0, nIdSim, nCmt), 
.   //                      tLagSim = rep_array(0.0, nIdSim, nCmt);
.   
.   real weightSim = 70,
.        ageSim = 35,
.        albuminSim = 4.5;
.   int nEGFR = 4;
.   array[nEGFR] real EGFRSim = {20, 40, 60, 90};
.   
.   for(i in 1:ntSim){
.     timeSim[i] = i - 1;
.   }
.   amtSim[{1, 25, 49, 73, 97, 121, 145}] = rep_array(25, 7);
.   evidSim[{1, 25, 49, 73, 97, 121, 145}] = rep_array(1, 7);
.   
. }
. 
. parameters{
.   real<lower = 0> CLHat, QHat, V2Hat, V3Hat;
. // To constrain kaHat > lambda1 uncomment the following
.   real<lower = (CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat +
.       sqrt((CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat)^2 -
.            4 * CLHat / V2Hat * QHat / V3Hat)) / 2> kaHat; // ka > lambda_1
.   real EGFR_CL, age_CL, albumin_CL;
.   
.   real<lower = 0> sigma;
.   vector<lower = 0>[nRandom] omega;
. //  corr_matrix[nRandom] rho;
. //  array[nId] vector[nRandom] theta;
.   cholesky_factor_corr[nRandom] L_corr;
.   matrix[nRandom, nId] z;
. }
. 
. transformed parameters{
.   
. }
. 
. model{
. 
. }
. 
. generated quantities{
.   vector[nRandom] thetaHat = log([CLHat, QHat, V2Hat, V3Hat, kaHat]');
.   // 5th, 50th & 95% percentiles of simulated concentrations
.   array[nEGFR, ntSim] real cPred5, cPred50, cPred95;
.   {
.     // Code block used so following declared variables are not saved
.     // to disk
.     
.     // Individual parameters for hypothetical new individuals
.     matrix[nRandom, nIdSim] zSim;
.     matrix[nIdSim, nRandom] thetaSim;
.     vector[nIdSim] CLSim, QSim, V2Sim, V3Sim, kaSim;
.     
.     row_vector[ntSim] cHatSim; // predicted concentration in new individuals
.     matrix[nCmt, ntSim] xSim; // mass in all compartments in new individuals
.     matrix[nIdSim, ntSim] cPredSim;
.     
.     // Simulations for posterior predictive checks
.     for(j in 1:nIdSim){
.       zSim[,j] = to_vector(normal_rng(rep_vector(0, nRandom), 1));
.     }
.     thetaSim = (rep_matrix(thetaHat, nIdSim) + diag_pre_multiply(omega, L_corr * zSim))';
.     QSim = exp(thetaSim[,2] + 0.75 * log(weightSim / 70));
.     V2Sim = exp(thetaSim[,3] + log(weightSim / 70));
.     V3Sim = exp(thetaSim[,4] + log(weightSim / 70));
.     kaSim = exp(thetaSim[,5]);
.     
.     for(i in 1:nEGFR){
.       CLSim = exp(thetaSim[,1] + 0.75 * log(weightSim / 70) +
.       EGFR_CL * log(EGFRSim[i] / 90) +
.       age_CL * log(ageSim / 35) +
.       albumin_CL * log(albuminSim / 4.5));
.       
.       for(j in 1:nIdSim){
.         xSim = pmx_solve_twocpt(timeSim,
.                                 amtSim,
.                                 rateSim,
.                                 iiSim,
.                                 evidSim,
.                                 cmtSim,
.                                 addlSim,
.                                 ssSim,
.                                 {CLSim[j], QSim[j], V2Sim[j], 
.                                 V3Sim[j], kaSim[j]});
.         
.         cHatSim = xSim[2,] / V2Sim[j];
.         cPredSim[j, 1] = 0.0;
.         cPredSim[j, 2:ntSim] = to_row_vector(lognormal_rng(log(cHatSim[2:ntSim]), 
.                                           sigma)); 
.       }
.       for(k in 1:ntSim){
.         cPred5[i, k] = quantile(cPredSim[,k], 0.05);
.         cPred50[i, k] = quantile(cPredSim[,k], 0.5);
.         cPred95[i, k] = quantile(cPredSim[,k], 0.95);
.       }
.     }
.   }
. }

ppkexpo5_gq2: Submit the model

## Set cmdstanr arguments
ppkexpo5_gq2 <- ppkexpo5_gq2 %>%
  set_stanargs(list(parallel_chains = 4,
                    seed = 1234),
               .clear = TRUE)

## Check that the necessary files are present
check_stan_model(ppkexpo5_gq2)

## Simulate using Stan
ppkexpo5_gq2_sim <- ppkexpo5_gq2 %>% submit_model(.overwrite = TRUE)

Plot posterior predictions of plasma drug concentrations as a function of time and renal function

model_name <- "ppkexpo5_gq2"
mod <- read_model(here(MODEL_DIR, model_name))
fit <- read_fit_model(mod)

ntSim <- 193
tSim <- seq(0, ntSim - 1)
EGFR <- c(20, 40, 60, 90)

sim1 <- spread_draws(fit, 
                     cPred5[iEGFR, itSim],
                     cPred50[iEGFR, itSim],
                     cPred95[iEGFR, itSim]) %>%
  mutate(time = tSim[itSim],
         EGFR = EGFR[iEGFR])

sim1_summary <- sim1 %>%
  group_by(time, EGFR) %>%
  summarize(lo_cPred5 = quantile(cPred5, 0.025),
            med_cPred5 = quantile(cPred5, 0.5),
            hi_cPred5 = quantile(cPred5, 0.975),
            lo_cPred50 = quantile(cPred50, 0.025),
            med_cPred50 = quantile(cPred50, 0.5),
            hi_cPred50 = quantile(cPred50, 0.975),
            lo_cPred95 = quantile(cPred95, 0.025),
            med_cPred95 = quantile(cPred95, 0.5),
            hi_cPred95 = quantile(cPred95, 0.975)) %>%
  ungroup

EGFR_plot <- ggplot(sim1_summary, aes(x = time, y = med_cPred50)) +
  geom_line(aes(x = time, y = med_cPred5, color = "5th & 95th percentiles")) +
  geom_ribbon(aes(ymin = lo_cPred5, ymax = hi_cPred5, 
                  fill = "5th & 95th percentiles"), alpha = 0.25) +
  geom_line(aes(x = time, y = med_cPred50, color = "median")) +
  geom_ribbon(aes(ymin = lo_cPred50, ymax = hi_cPred50, 
                  fill = "median"), alpha = 0.25) +
  geom_line(aes(x = time, y = med_cPred95, color = "5th & 95th percentiles")) +
  geom_ribbon(aes(ymin = lo_cPred95, ymax = hi_cPred95, 
                  fill = "5th & 95th percentiles"), alpha = 0.25) +
  scale_color_brewer(name  ="median & 95 % CI",
                     breaks=c("median", "5th & 95th percentiles"),
                     palette = "Set1") +
  scale_fill_brewer(name  ="median & 95 % CI",
                     breaks=c("median", "5th & 95th percentiles"),
                    palette = "Set1") +
##  scale_y_log10() +
  labs(x = "time (h)",
       y = "plasma drug concentration (mg/L)") +
  theme(text = element_text(size = 12),
        axis.text = element_text(size = 8),
        legend.position = "bottom",
        strip.text = element_text(size = 8)) +
  facet_wrap(~ EGFR)
EGFR_plot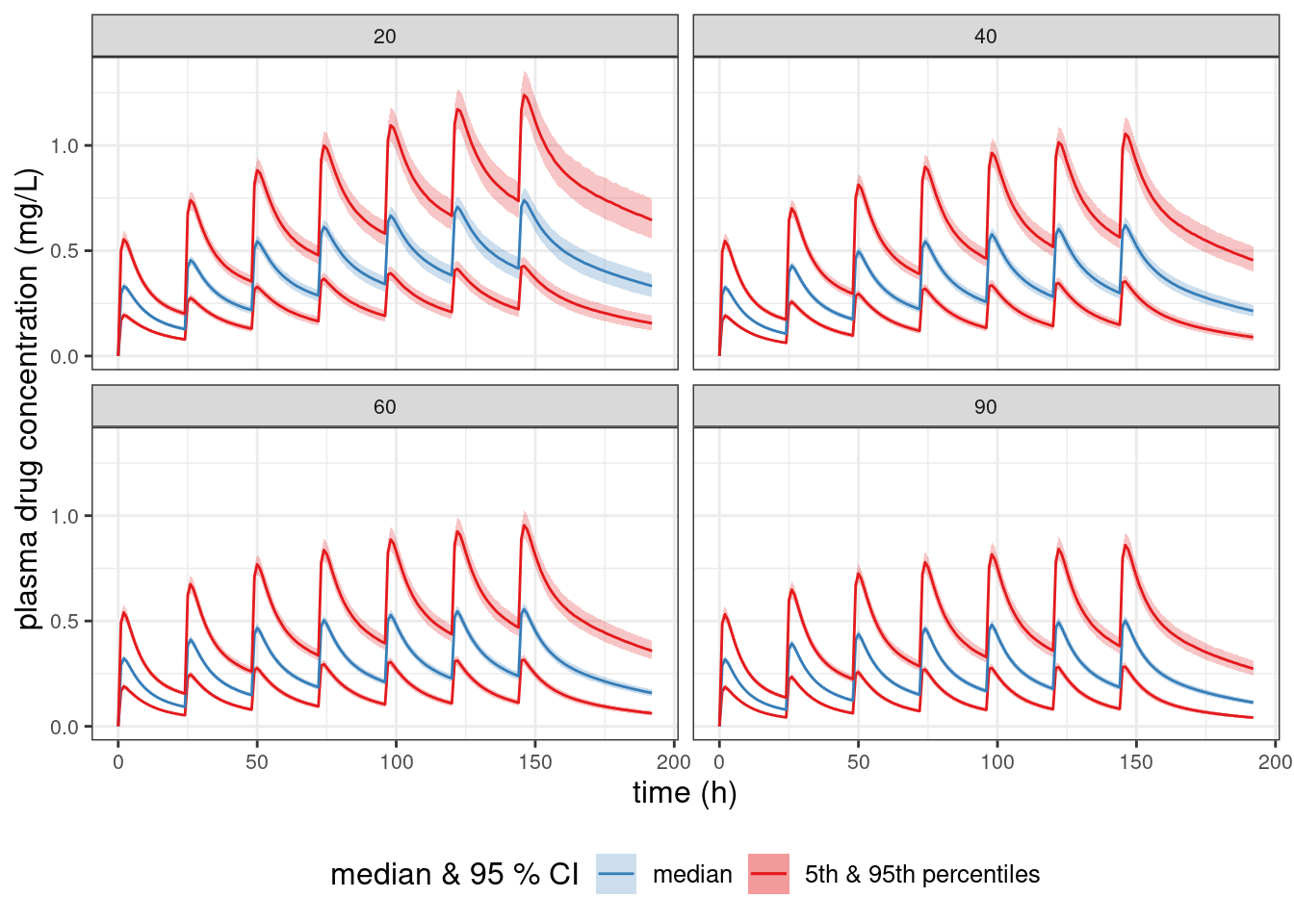

Figure 3: Posterior predictions of plasma drug concentrations as a function of time and renal function (EGFR).

Other resources

The following script from the GitHub repository is discussed on this page. If you’re interested running this code, visit the About the GitHub Repo page first.

Generated Quantities script: generated-quantities.Rmd