library(bbr)
library(bbr.bayes)
library(here)
library(tidyverse)
library(yspec)
library(cmdstanr)
library(posterior)
library(bayesplot)
library(tidybayes)
library(glue)
library(kableExtra)
set_cmdstan_path(path = here("Torsten", "v0.91.0", "cmdstan"))
MODEL_DIR <- here("model", "stan")
FIGURE_DIR <- here("deliv", "figure")Introduction
Stan provides mechanisms for parallel computation within each Markov Chain Monte Carlo (MCMC) using either multi-threading or message passing interface (MPI). Let’s see how we can do this for our population pharmacokinetic (popPK) example. We use multi-threading which requires we modify the Stan model so it uses the reduce_sum function for calculating the overall log-probability. Meaning, we need to write a user-defined Stan function to calculate the log-probability for the data from a subset of individuals. It also requires that Torsten and the model file be compiled with cpp_options = list(stan_threads = TRUE).
The results shown here were run on a computer with 64 vCPUs, allowing for simultaneous running up to four chains with 16 threads/chain.
The page demonstrates how to:
- Revise Stan/Torsten popPK models to permit within-chain parallel computation using multi-threading
- Compile and execute Stan/Torsten models to use multi-threading
Tools used
MetrumRG packages
bbr Manage, track, and report modeling activities, through simple R objects, with a user-friendly interface between R and NONMEM®.
bbr.bayes Extension of the bbr package to support Bayesian modeling with Stan or NONMEM®.
CRAN packages
dplyr A grammar of data manipulation.
Set up
Load required packages and set file paths to your model and figure directories.
Revise model to use multi-threading
Let’s modify ppkexpo5 to use reduce_sum and call it ppkexpo5_rs1.
ppkexpo5 <- read_model(here(MODEL_DIR, "ppkexpo5"))
ppkexpo5_rs1 <- copy_model_from(ppkexpo5, "ppkexpo5_rs1", .inherit_tags = TRUE,
.overwrite = TRUE) %>%
add_description("PopPK model: ppkexpo5 using reduce_sum")Now, manually edit ppkexpo5_rs1.stan to implement reduce_sum. Recall that Stan calculates the sum of log probabilities over all the levels of a hierarchical model. In our case, there are three such levels: the prior distributions, the individual-level random effects, and the observed data. To use reduce_sum, we need to create a Stan function that calculates the sum of log probabilities for a subset of individuals. That requires a bit of book-keeping in the code and some changes to the data. That means we also need to edit ppkexpo5_rs1-standata.R.
For this demo, we copy previously created files from the demo folder.
ppkexpo5_rs1 <- ppkexpo5_rs1 %>%
add_stanmod_file(here(MODEL_DIR, "demo", "ppkexpo5_rs1.stan")) %>%
add_standata_file(here(MODEL_DIR, "demo", "ppkexpo5_rs1-standata.R"))There are two forms of the reduce_sum function: reduce_sum and reduce_sum_static. reduce_sum uses a dynamic scheduling algorithm to automatically partition the individuals for parallel computation, so the partitioning changes from one iteration to the next. A consequence of this is that the results are not strictly reproducible. On the other hand, reduce_sum_static always partitions the individuals the same way each time for a given data set and grainsize (the maximum number of individuals in each partition). Since we want reproducibility of our analyses, we use reduce_sum_static.
Here is the resulting Stan model ppkexpo5_rs1:
. /*
. Final PPK model
. - Linear 2 compartment
. - Non-centered parameterization
. - lognormal residual variation
. - Allometric scaling
. - Additional covariates: EGFR, age, albumin
. - reduce_sum
.
. Based on NONMEM PopPK FOCE example project
. */
.
. functions{
. real partial_sum(array[] int id,
. int id_start, int id_end,
. vector cObs,
. array[] int blq,
. real LOQ,
. array[] int start, array[] int end,
. int nCmt,
. array[] real time,
. array[] real amt,
. array[] real rate,
. array[] real ii,
. array[] int evid,
. array[] int cmt,
. array[] int addl,
. array[] int ss,
. vector CL,
. vector Q,
. vector V2,
. vector V3,
. vector ka,
. real sigma
. ){
. int nt = end[id_end] - start[id_start] + 1;
. row_vector[nt] cHat; // predicted concentration
. matrix[nCmt, nt] x; // mass in all compartments
. real result;
.
. for(j in id_start:id_end){
. x[, (start[j] - start[id_start] + 1):(end[j] - start[id_start] + 1)] =
. pmx_solve_twocpt(time[start[j]:end[j]],
. amt[start[j]:end[j]],
. rate[start[j]:end[j]],
. ii[start[j]:end[j]],
. evid[start[j]:end[j]],
. cmt[start[j]:end[j]],
. addl[start[j]:end[j]],
. ss[start[j]:end[j]],
. {CL[j], Q[j], V2[j], V3[j], ka[j]});
.
. cHat[(start[j] - start[id_start] + 1):(end[j] - start[id_start] + 1)] =
. x[2, (start[j] - start[id_start] + 1):(end[j] - start[id_start] + 1)] / V2[j];
. }
.
. // likelihood
. result = 0;
. for(i in start[id_start]:end[id_end]){
. if(cObs[i] > 0)
. result += lognormal_lpdf(cObs[i] | log(cHat[i - start[id_start] + 1]), sigma);
. else if(blq[i] == 1)
. result += lognormal_lcdf(LOQ | log(cHat[i - start[id_start] + 1]), sigma);
. }
.
. return result;
. }
. }
.
. data{
. int<lower = 1> nId; // number of individuals
. int<lower = 1> nt; // number of events (rows in data set)
. array[nt] real<lower = 0> amt, time;
. array[nt] int<lower = 1> cmt;
. array[nt] int<lower = 0> evid;
. array[nId] int<lower = 1> start, end; // indices of first & last events
. vector<lower = 0>[nId] weight, EGFR, age, albumin;
. vector<lower = -1>[nt] cObs;
. array[nt] int<lower = 0, upper = 1> blq;
. real<lower = 0> LOQ;
. int grainsize;
. }
.
. transformed data{
. int<lower = 1> nRandom = 5, nCmt = 3;
. array[nt] real<lower = 0> rate = rep_array(0.0, nt),
. ii = rep_array(0.0, nt);
. array[nt] int<lower = 0> addl = rep_array(0, nt),
. ss = rep_array(0, nt);
. array[nId, nCmt] real F = rep_array(1.0, nId, nCmt),
. tLag = rep_array(0.0, nId, nCmt);
. array[nId] int id;
.
. for(i in 1:nId) id[i] = i;
. }
.
. parameters{
. real<lower = 0> CLHat, QHat, V2Hat, V3Hat;
. // To constrain kaHat > lambda1 uncomment the following
. real<lower = (CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat +
. sqrt((CLHat / V2Hat + QHat / V2Hat + QHat / V3Hat)^2 -
. 4 * CLHat / V2Hat * QHat / V3Hat)) / 2> kaHat; // ka > lambda_1
. real EGFR_CL, age_CL, albumin_CL;
.
. real<lower = 0> sigma;
. vector<lower = 0>[nRandom] omega;
. cholesky_factor_corr[nRandom] L_corr;
. matrix[nRandom, nId] z;
. }
.
. transformed parameters{
. vector[nRandom] thetaHat = log([CLHat, QHat, V2Hat, V3Hat, kaHat]');
. // Individual parameters
. matrix[nId, nRandom] theta = (rep_matrix(thetaHat, nId) + diag_pre_multiply(omega, L_corr * z))';
. vector<lower = 0>[nId] CL = exp(theta[,1] + 0.75 * log(weight / 70) +
. EGFR_CL * log(EGFR / 90) +
. age_CL * log(age / 35) +
. albumin_CL * log(albumin / 4.5)),
. Q = exp(theta[,2] + 0.75 * log(weight / 70)),
. V2 = exp(theta[,3] + log(weight / 70)),
. V3 = exp(theta[,4] + log(weight / 70)),
. ka = exp(theta[,5]);
. corr_matrix[nRandom] rho = L_corr * L_corr';
.
. }
.
. model{
. // priors
. CLHat ~ normal(0, 10);
. QHat ~ normal(0, 10);
. V2Hat ~ normal(0, 50);
. V3Hat ~ normal(0, 100);
. kaHat ~ normal(0, 3);
. EGFR_CL ~ normal(0, 2);
. age_CL ~ normal(0, 2);
. albumin_CL ~ normal(0, 2);
.
. sigma ~ normal(0, 0.5);
. omega ~ normal(0, 0.5);
. L_corr ~ lkj_corr_cholesky(2);
.
. // interindividual variability
. to_vector(z) ~ normal(0, 1);
.
. // likelihood
. target += reduce_sum_static(partial_sum, id, grainsize, cObs, blq, LOQ, start, end,
. nCmt, time, amt, rate, ii, evid, cmt, addl, ss, CL, Q, V2, V3, ka, sigma);
.
. }
.
. generated quantities{
.
. }The key difference from ppkexpo5 is that much of the code in the transformed parameters block has been moved into the function called partial_sum which is defined in the functions block. We can see that even more clearly using the model_diff function. By default, the model is compared to the model which it was based on (in this case, ppkexpo5).
model_diff(ppkexpo5_rs1). < ppkexpo5_rs1 > ppkexpo5
. @@ 6,78 @@ @@ 6,22 @@
. - Allometric scaling - Allometric scaling
. - Additional covariates: EGFR, age, - Additional covariates: EGFR, age,
. albumin albumin
. < - reduce_sum ~
.
. Based on NONMEM PopPK FOCE example pr Based on NONMEM PopPK FOCE example pr
. oject oject
. */ */
.
. < functions{ ~
. < real partial_sum(array[] int id, ~
. < int id_start, int id_end, ~
. < vector cObs, ~
. < array[] int blq, ~
. < real LOQ, ~
. < array[] int start, array[] int end, ~
. < int nCmt, ~
. < array[] real time, ~
. < array[] real amt, ~
. < array[] real rate, ~
. < array[] real ii, ~
. < array[] int evid, ~
. < array[] int cmt, ~
. < array[] int addl, ~
. < array[] int ss, ~
. < vector CL, ~
. < vector Q, ~
. < vector V2, ~
. < vector V3, ~
. < vector ka, ~
. < real sigma ~
. < ){ ~
. < int nt = end[id_end] - start[id_s ~
. : tart] + 1; ~
. < row_vector[nt] cHat; // predicted ~
. : concentration ~
. < matrix[nCmt, nt] x; // mass in al ~
. : l compartments ~
. < real result; ~
. < ~
. < for(j in id_start:id_end){ ~
. < x[, (start[j] - start[id_start] ~
. : + 1):(end[j] - start[id_start] + 1)] ~
. : = ~
. < pmx_solve_twocpt(time[start[j ~
. : ]:end[j]], ~
. < amt[start[j]:end[j]], ~
. < rate[start[j]:end[j]], ~
. < ii[start[j]:end[j]], ~
. < evid[start[j]:end[j]], ~
. < cmt[start[j]:end[j]], ~
. < addl[start[j]:end[j]], ~
. < ss[start[j]:end[j]], ~
. < {CL[j], Q[j], V2[j], V3[j], k ~
. : a[j]}); ~
. < ~
. < cHat[(start[j] - start[id_start ~
. : ] + 1):(end[j] - start[id_start] + 1) ~
. : ] = ~
. < x[2, (start[j] - start[id_sta ~
. : rt] + 1):(end[j] - start[id_start] + ~
. : 1)] / V2[j]; ~
. < } ~
. < ~
. < // likelihood ~
. < result = 0; ~
. < for(i in start[id_start]:end[id_e ~
. : nd]){ ~
. < if(cObs[i] > 0) ~
. < result += lognormal_lpdf(cObs ~
. : [i] | log(cHat[i - start[id_start] + ~
. : 1]), sigma); ~
. < else if(blq[i] == 1) ~
. < result += lognormal_lcdf(LOQ ~
. : | log(cHat[i - start[id_start] + 1]), ~
. : sigma); ~
. < } ~
. < ~
. < return result; ~
. < } ~
. < } ~
. < ~
. data{ data{
. int<lower = 1> nId; // number of in int<lower = 1> nId; // number of in
. dividuals dividuals
. int<lower = 1> nt; // number of eve int<lower = 1> nt; // number of eve
. nts (rows in data set) nts (rows in data set)
. ~ > int<lower = 1> nObs; // number of P
. ~ : K observations
. ~ > array[nObs] int<lower = 1> iObs; //
. ~ : event indices for PK observations
. ~ > int<lower = 1> nBlq; // number of B
. ~ : LQ observations
. ~ > array[nBlq] int<lower = 1> iBlq; //
. ~ : event indices for BLQ observations
. array[nt] real<lower = 0> amt, time array[nt] real<lower = 0> amt, time
. ; ;
. array[nt] int<lower = 1> cmt; array[nt] int<lower = 1> cmt;
. array[nt] int<lower = 0> evid; array[nt] int<lower = 0> evid;
. < array[nId] int<lower = 1> start, en > array[nId] int<lower = 1> start, en
. : d; // indices of first & last events : d; // indices of first & last observa
. ~ : tions
. vector<lower = 0>[nId] weight, EGFR vector<lower = 0>[nId] weight, EGFR
. , age, albumin; , age, albumin;
. < vector<lower = -1>[nt] cObs; > vector<lower = 0>[nObs] cObs;
. < array[nt] int<lower = 0, upper = 1> ~
. : blq; ~
. real<lower = 0> LOQ; real<lower = 0> LOQ;
. < int grainsize; ~
. } }
.
. @@ 90,7 @@ @@ 34,4 @@
. array[nId, nCmt] real F = rep_array array[nId, nCmt] real F = rep_array
. (1.0, nId, nCmt), (1.0, nId, nCmt),
. tLag = rep_ar tLag = rep_ar
. ray(0.0, nId, nCmt); ray(0.0, nId, nCmt);
. < array[nId] int id; ~
. < ~
. < for(i in 1:nId) id[i] = i; ~
. } }
.
. @@ 105,4 @@ @@ 46,6 @@
. real<lower = 0> sigma; real<lower = 0> sigma;
. vector<lower = 0>[nRandom] omega; vector<lower = 0>[nRandom] omega;
. ~ > // corr_matrix[nRandom] rho;
. ~ > // array[nId] vector[nRandom] theta;
. cholesky_factor_corr[nRandom] L_cor cholesky_factor_corr[nRandom] L_cor
. r; r;
. matrix[nRandom, nId] z; matrix[nRandom, nId] z;
. @@ 122,6 @@ @@ 65,22 @@
. ka = exp(the ka = exp(the
. ta[,5]); ta[,5]);
. corr_matrix[nRandom] rho = L_corr corr_matrix[nRandom] rho = L_corr
. * L_corr'; * L_corr';
. ~ >
. ~ > row_vector[nt] cHat; // predicted c
. ~ : oncentration
. ~ > matrix[nCmt, nt] x; // mass in all
. ~ : compartments
.
. ~ > for(j in 1:nId){
. ~ > x[, start[j]:end[j]] = pmx_solve_
. ~ : twocpt(time[start[j]:end[j]],
. ~ >
. ~ : amt[start[j]:end[j]],
. ~ >
. ~ : rate[start[j]:end[j]],
. ~ >
. ~ : ii[start[j]:end[j]],
. ~ >
. ~ : evid[start[j]:end[j]],
. ~ >
. ~ : cmt[start[j]:end[j]],
. ~ >
. ~ : addl[start[j]:end[j]],
. ~ >
. ~ : ss[start[j]:end[j]],
. ~ >
. ~ : {CL[j], Q[j], V2[j], V3[j], ka
. ~ : [j]});
. ~ >
. ~ > cHat[start[j]:end[j]] = x[2, star
. ~ : t[j]:end[j]] / V2[j];
. } }
. ~ > }
.
. model{ model{
. @@ 144,6 @@ @@ 103,6 @@
.
. // likelihood // likelihood
. < target += reduce_sum_static(partial > cObs ~ lognormal(log(cHat[iObs]), s
. : _sum, id, grainsize, cObs, blq, LOQ, : igma); // observed data likelihood
. : start, end, ~
. < nCmt, time, amt, rate, ii > target += lognormal_lcdf(LOQ | log(
. : , evid, cmt, addl, ss, CL, Q, V2, V3, : cHat[iBlq]), sigma); // BLQ data like
. : ka, sigma); : lihood
.
. } }Here is the ppkexpo5_rs1-standata.R file:
. # Create Stan data
. #
. # This function must return the list that will be passed to `data` argument
. # of `cmdstanr::sample()`
. #
. # The `.dir` argument represents the absolute path to the directory containing
. # this file. This is useful for building file paths to the input files you will
. # load. Note: you _don't_ need to pass anything to this argument, you only use
. # it within the function. `bbr` will pass in the correct path when it calls
. # `make_standata()` under the hood.
. make_standata <- function(.dir) {
. # read in any input data
. data1 <- readr::read_csv(file.path(.dir, '..', '..', '..', "data", "derived",
. "pk.csv"), na = ".") %>%
. mutate(AMT = if_else(is.na(AMT), 0, AMT),
. idSeq = as.numeric(ordered(ID, levels = unique(ID))))
.
. ## Write data1 to file in model directory
. saveRDS(data1, file = file.path(.dir, "data1.RData"))
.
. grainsize <- readRDS(file.path(.dir, "grainsize.RDS"))
.
. nt <- nrow(data1)
. start <- (1:nt)[!duplicated(data1$ID)]
. end <- c(start[-1] - 1, nt)
. nId <- length(unique(data1$ID))
.
. stan_data <- with(data1,
. list(nId = nId,
. nt = nt,
. amt = 1000 * AMT,
. cmt = CMT,
. evid = EVID,
. time = TIME,
. start = start,
. end = end,
. weight = WT[start],
. EGFR = EGFR[start],
. age = AGE[start],
. albumin = ALB[start],
. ## cObs = -1 if missing or not an observation record
. cObs = if_else(BLQ == 0 & EVID == 0, DV, -1),
. blq = BLQ,
. LOQ = 10,
. grainsize = grainsize
. ))
. return(stan_data)
. }And how it differs from the ppkexpo5-standata.R file:
model_diff(ppkexpo5_rs1, .file = "standata"). < ppkexpo5_rs1-standata > ppkexpo5-standata
. @@ 13,11 @@ @@ 13,8 @@
. data1 <- readr::read_csv(file.path( data1 <- readr::read_csv(file.path(
. .dir, '..', '..', '..', "data", "deri .dir, '..', '..', '..', "data", "deri
. ved", ved",
.
. "pk.csv"), na = ".") %>% "pk.csv"), na = ".") %>%
. < mutate(AMT = if_else(is.na(AMT), > mutate(AMT = if_else(is.na(AMT),
. : 0, AMT), : 0, AMT))
. < idSeq = as.numeric(ordered ~
. : (ID, levels = unique(ID)))) ~
.
. ## Write data1 to file in model dir ## Write data1 to file in model dir
. ectory ectory
. < saveRDS(data1, file = file.path(.di > save(data1, file = file.path(.dir,
. : r, "data1.RData")) : "data1.RData"))
. < ~
. < grainsize <- readRDS(file.path(.dir ~
. : , "grainsize.RDS")) ~
.
. nt <- nrow(data1) nt <- nrow(data1)
. @@ 26,7 @@ @@ 23,18 @@
. nId <- length(unique(data1$ID)) nId <- length(unique(data1$ID))
.
. ~ > ## Indices of records containing ob
. ~ : served data
. ~ > iObs <- with(data1, (1:nrow(data1))
. ~ : [BLQ == 0 & EVID == 0])
. ~ > nObs <- length(iObs)
. ~ > ## Indices of records containing BQ
. ~ : L concentrations
. ~ > iBlq <- with(data1, (1:nrow(data1))
. ~ : [BLQ == 1 & EVID == 0])
. ~ > nBlq <- length(iBlq)
. ~ >
. stan_data <- with(data1, stan_data <- with(data1,
. list(nId = nId, list(nId = nId,
. nt = nt, nt = nt,
. ~ > nObs = nObs,
. ~ > iObs = iObs,
. ~ > nBlq = nBlq,
. ~ > iBlq = iBlq,
. amt = 1000 * amt = 1000 *
. AMT, AMT,
. cmt = CMT, cmt = CMT,
. @@ 39,9 @@ @@ 47,6 @@
. age = AGE[st age = AGE[st
. art], art],
. albumin = AL albumin = AL
. B[start], B[start],
. < ## cObs = -1 > cObs = DV[iO
. : if missing or not an observation rec : bs],
. : ord ~
. < cObs = if_el ~
. : se(BLQ == 0 & EVID == 0, DV, -1), ~
. < blq = BLQ, ~
. < LOQ = 10, > LOQ = 10
. < grainsize = ~
. : grainsize ~
. )) ))
. return(stan_data) return(stan_data)The handling of grainsize is worth a few comments. Its value may be set by hard-coding in the transformed data block of the model or by passing it in through the data set. For this example, we pass it via the data set. We could do that when we manually edit the -standata.R file; however, we do something a little different so we can automatically loop over a range of gransize values and change the value of grainsize in the -standata.R file without manual editing. We write the grainsize value to a file in the model folders. The corresponding -standata.R files read the grainsize value from those files at run time. That’s the reason behind the following statement in the -standata.R file.
grainsize <- readRDS(file.path(.dir, "grainsize.RDS"))
Submit the model
Once we have a model that enables multi-threading (i.e., a model that uses reduce_sum), model submission is almost the same as before. Key differences are:
- Setting the
STAN_NUM_THREADSenvironmental variable - Setting the
threads_per_chainargument ofset_stanargs - Calculating the value of grainsize and writing it to a file in the model folder
Let’s start with two threads per chain.
threads_per_chain <- 2
## There is a bug in the current bbr.bayes version that prevents threading when the
## model is compiled by submit_model amd STAN_NUM_THREADS is not set by some other
## mechanism. (Issue 59)
Sys.setenv(STAN_NUM_THREADS = threads_per_chain)
## Set cmdstanr arguments
ppkexpo5_rs1 <- ppkexpo5_rs1 %>%
set_stanargs(list(iter_warmup = 500,
iter_sampling = 500,
thin = 1,
chains = 4,
parallel_chains = 4,
threads_per_chain = threads_per_chain,
seed = 1234,
save_warmup = FALSE),
.clear = TRUE)
## Write the value of the grainsize paraneter of reduce_sum to a file.
grainsize <- round(160 / threads_per_chain)
saveRDS(grainsize, file = here::here("model", "stan", "ppkexpo5_rs1", "grainsize.RDS"))
## Fit the model using Stan
ppkexpo5_rs1_fit <- ppkexpo5_rs1 %>% submit_model(.overwrite = TRUE)If the model has already been fitted, you can read it using the following statements without having to refit the model.
ppkexpo5_rs1 <- read_model(here(MODEL_DIR, "ppkexpo5_rs1"))
ppkexpo5_rs1_fit <- read_fit_model(ppkexpo5_rs1)Now, loop over a range of threads_per_chain values to explore how the number of threads affects the computation time.
threads_per_chain <- c(2, 4, 8, 16)
for(i in 2:length(threads_per_chain)){
assign(paste0("ppkexpo5_rs", i),
copy_model_from(ppkexpo5_rs1, paste0("ppkexpo5_rs", i), .inherit_tags = TRUE,
.overwrite = TRUE))
Sys.setenv(STAN_NUM_THREADS = threads_per_chain[i])
## Set cmdstanr arguments
assign(paste0("ppkexpo5_rs", i),
get(paste0("ppkexpo5_rs", i)) %>%
set_stanargs(list(iter_warmup = 500,
iter_sampling = 500,
thin = 1,
chains = 4,
parallel_chains = 4,
threads_per_chain = threads_per_chain[i],
seed = 1234,
save_warmup = FALSE),
.clear = TRUE) %>%
add_description("PopPK model: ppkexpo5 using reduce_sum"))
## Write the value of the grainsize paraneter of reduce_sum to a file.
grainsize <- round(160 / threads_per_chain[i])
saveRDS(grainsize, file = here::here("model", "stan", paste0("ppkexpo5_rs", i),
"grainsize.RDS"))
## Fit the model using Stan
assign(paste0("ppkexpo5_rs", i, "_fit"),
get(paste0("ppkexpo5_rs", i)) %>% submit_model(.overwrite = TRUE))
}If the models have already been fitted, you can read them using the following statements without having to refit the models.
for(i in 2:4){
assign(paste0("ppkexpo5_rs", i),
read_model(here(MODEL_DIR, paste0("ppkexpo5_rs", i))))
assign(paste0("ppkexpo5_rs", i, "_fit"),
read_fit_model(here(MODEL_DIR, paste0("ppkexpo5_rs", i))))
}Now, we can use the stan_summary_log function to tabulate the run times.
## threads_per_chain <- c(1, 2, 4, 8, 16)
## Summary log
sum_log_rs <- stan_summary_log(MODEL_DIR) %>%
filter(grepl("ppkexpo5", run)) %>%
filter(!grepl("_gq", run))
sum_log_rs <- sum_log_rs %>%
mutate(total_time = list_simplify(map(fit, ~.$time()$total)),
threads_per_chain = list_simplify(map(fit, ~.$metadata()$threads_per_chain)))
sum_log_rs %>%
select(run, iter_warmup, iter_sampling, threads_per_chain, total_time) %>%
mutate(total_time = pmtables::sig(total_time / 60, 3)) %>%
rename("total_time (min)" = total_time) %>%
arrange(threads_per_chain) %>%
knitr::kable() %>%
kable_styling()| run | iter_warmup | iter_sampling | threads_per_chain | total_time (min) |
|---|---|---|---|---|
| ppkexpo5 | 500 | 500 | 1 | 60.8 |
| ppkexpo5_rs1 | 500 | 500 | 2 | 32.1 |
| ppkexpo5_rs2 | 500 | 500 | 4 | 20.2 |
| ppkexpo5_rs3 | 500 | 500 | 8 | 11.6 |
| ppkexpo5_rs4 | 500 | 500 | 16 | 8.83 |
time_data <- sum_log_rs %>%
select(threads_per_chain, total_time) %>%
arrange(threads_per_chain)
run_time_plot <- ggplot(time_data, aes(x = threads_per_chain, y = total_time / 60)) +
geom_line() +
scale_y_log10() +
labs(x = "threads/chain",
y = "time (min)")# show plot in HTML output
run_time_plot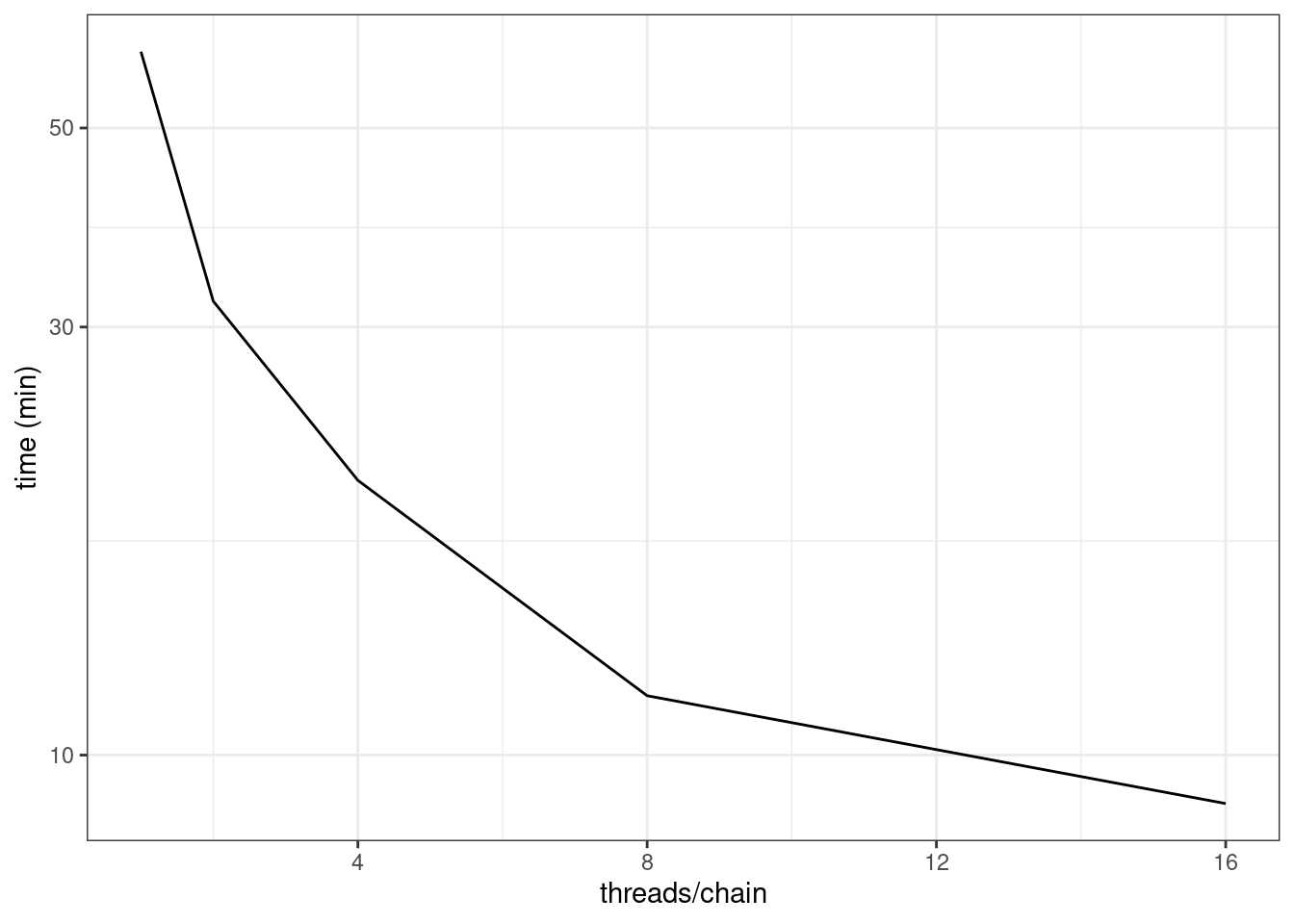
We see that going from one to 16 threads per chain reduces the run time from 60.8 minutes to 8.83 minutes.
Other resources
The following script from the GitHub repository is discussed on this page. If you’re interested running this code, visit the About the GitHub Repo page first.
Parallel Computation script: parallel-computation.Rmd