MCMC Diagnostics

Example MCMC diagnostics with bbr.bayes.

bbr.bayes
diagnostics

Introduction

In this Expo, we make the distinction between two types of diagnostics:

  • Markov Chain Monte Carlo (MCMC) convergence diagnostics
  • Model diagnostics, aka, goodness-of-fit (GOF) diagnostics

This page demonstrates the use of bbr.bayes, and other tools, to generate MCMC diagnostics for Stan/Torsten Bayesian (Bayes) models.

There is no explicit functionality in bbr.bayes to perform these steps; however, the output from bbr.bayes makes these steps relatively simple.

Tools used

MetrumRG packages

bbr Manage, track, and report modeling activities, through simple R objects, with a user-friendly interface between R and NONMEM®.

bbr.bayes Extension of the bbr package to support Bayesian modeling with Stan or NONMEM®.

CRAN packages

dplyr A grammar of data manipulation.

bayesplot Plotting Bayesian models and diagnostics with ggplot.

posterior Provides tools for working with output from Bayesian models, including output from CmdStan.

Set up

Load required packages and set file paths to your model and figure directories.

library(bbr)
library(bbr.bayes)
library(here)
library(tidyverse)
library(posterior)
library(bayesplot)
library(glue)
library(kableExtra)

cmdstanr::set_cmdstan_path(path = here("Torsten", "v0.91.0", "cmdstan"))

source(here("script", "mcmc-diagnostic-functions.R"))

MODEL_DIR <- here("model", "stan")

bayesplot::color_scheme_set('viridis')
theme_set(theme_bw())

MCMC diagnostics

After fitting the model, we examine a suite of MCMC diagnostics to see if anything is amiss with the sampling. Focus on split Rhat, bulk and tail ESS (effective sample size), trace plots, and density plots. If any of these raise a flag about convergence, then additional diagnostics would be examined.

Model summary

We begin by reading in the output from our first base model, ppkexpo1. This is done using the read_fit_model function from bbr.bayes which returns a CmdStanMCMC object that provides several methods for querying the fitting results. For example, fit$draws() returns a draws array containing the MCMC samples.

model_name <- "ppkexpo1"
mod <- read_model(here(MODEL_DIR, model_name))
fit <- read_fit_model(mod)

fit$cmdstan_diagnose()
. Processing csv files: /data/expos/expo4-torsten-poppk/model/stan/ppkexpo1/ppkexpo1-output/ppkexpo1-202409271413-1-0c80d9.csv, /data/expos/expo4-torsten-poppk/model/stan/ppkexpo1/ppkexpo1-output/ppkexpo1-202409271413-2-0c80d9.csv, /data/expos/expo4-torsten-poppk/model/stan/ppkexpo1/ppkexpo1-output/ppkexpo1-202409271413-3-0c80d9.csv, /data/expos/expo4-torsten-poppk/model/stan/ppkexpo1/ppkexpo1-output/ppkexpo1-202409271413-4-0c80d9.csv
. 
. Checking sampler transitions treedepth.
. Treedepth satisfactory for all transitions.
. 
. Checking sampler transitions for divergences.
. No divergent transitions found.
. 
. Checking E-BFMI - sampler transitions HMC potential energy.
. The E-BFMI, 0.09, is below the nominal threshold of 0.30 which suggests that HMC may have trouble exploring the target distribution.
. If possible, try to reparameterize the model.
. 
. Effective sample size satisfactory.
. 
. The following parameters had split R-hat greater than 1.05:
.   omega[2], omega[4], theta[138,2], Q[138], Omega[2,2], Omega[4,2], Omega[2,4], Omega[4,4]
. Such high values indicate incomplete mixing and biased estimation.
. You should consider regularizating your model with additional prior information or a more effective parameterization.
. 
. Processing complete.
pars <- c("CLHat", "QHat", "V2Hat", "V3Hat", "kaHat",
          "sigma", glue("omega[{1:5}]"),
          paste0("rho[", matrix(apply(expand.grid(1:5, 1:5),
                                      1, paste, collapse = ","),
                                ncol = 5)[upper.tri(diag(5), 
                                                    diag = FALSE)], "]"))
# Get posterior samples for parameters of interest
posterior <- fit$draws(variables = pars)
# Get quantities related to NUTS performance, e.g., occurrence of
# divergent transitions
np <- nuts_params(fit) 

n_iter <- dim(posterior)[1]
n_chains <- dim(posterior)[2]

draws_sum <- fit$summary(variables = pars)
ptable <- draws_sum %>%
  mutate(across(-variable, ~ pmtables::sig(.x, maxex = 4))) %>% 
  rename(parameter = variable) %>%
  mutate("90% CI" = paste("(", q5, ", ", q95, ")", 
                          sep = "")) %>%
  select(parameter, mean, median, sd, mad, "90% CI", ess_bulk, ess_tail, rhat)

ptable %>% 
  kable %>%
  kable_styling()
parameter mean median sd mad 90% CI ess_bulk ess_tail rhat
CLHat 3.11 3.11 0.113 0.109 (2.93, 3.30) 2460 1570 1.00
QHat 3.80 3.80 0.178 0.187 (3.52, 4.09) 118 192 1.02
V2Hat 60.9 60.8 2.23 2.24 (57.3, 64.6) 278 494 1.00
V3Hat 67.7 67.7 1.87 1.90 (64.7, 70.8) 334 990 1.00
kaHat 1.61 1.60 0.117 0.116 (1.43, 1.82) 340 778 1.00
sigma 0.214 0.214 0.00304 0.00297 (0.208, 0.219) 2000 1600 1.00
omega[1] 0.436 0.435 0.0250 0.0254 (0.397, 0.479) 2380 1620 1.00
omega[2] 0.131 0.123 0.0609 0.0657 (0.0406, 0.234) 18.8 42.1 1.17
omega[3] 0.377 0.376 0.0266 0.0283 (0.335, 0.421) 412 1200 1.01
omega[4] 0.182 0.182 0.0291 0.0288 (0.135, 0.231) 66.6 413 1.05
omega[5] 0.545 0.543 0.0709 0.0713 (0.433, 0.667) 183 470 1.01
rho[1,2] -0.132 -0.152 0.268 0.270 (-0.549, 0.339) 184 381 1.02
rho[1,3] 0.676 0.680 0.0604 0.0607 (0.576, 0.771) 172 572 1.02
rho[2,3] 0.0912 0.0820 0.275 0.299 (-0.349, 0.547) 168 383 1.02
rho[1,4] 0.332 0.337 0.137 0.136 (0.0958, 0.543) 348 787 1.01
rho[2,4] 0.366 0.409 0.268 0.274 (-0.122, 0.748) 126 325 1.04
rho[3,4] 0.546 0.552 0.154 0.162 (0.286, 0.793) 113 148 1.03
rho[1,5] 0.600 0.607 0.0880 0.0911 (0.451, 0.737) 486 863 1.01
rho[2,5] -0.387 -0.435 0.303 0.290 (-0.820, 0.196) 81.2 191 1.04
rho[3,5] 0.436 0.443 0.107 0.109 (0.253, 0.593) 236 401 1.01
rho[4,5] -0.103 -0.111 0.196 0.203 (-0.417, 0.220) 128 349 1.02

For the population-level parameters, the Rhat values are less than or equal to 1.05 except for omega[2]. Also, some ESS bulk and tail values are on the low side. In addition, a couple divergent transitions occurred.

Rhat plot

We visualize the Rhat values with the mcmc_rhat function from bayesplot.

rhats <- draws_sum$rhat
names(rhats) <- draws_sum$variable
rhat_plot <- mcmc_rhat(rhats) + yaxis_text()
rhat_plot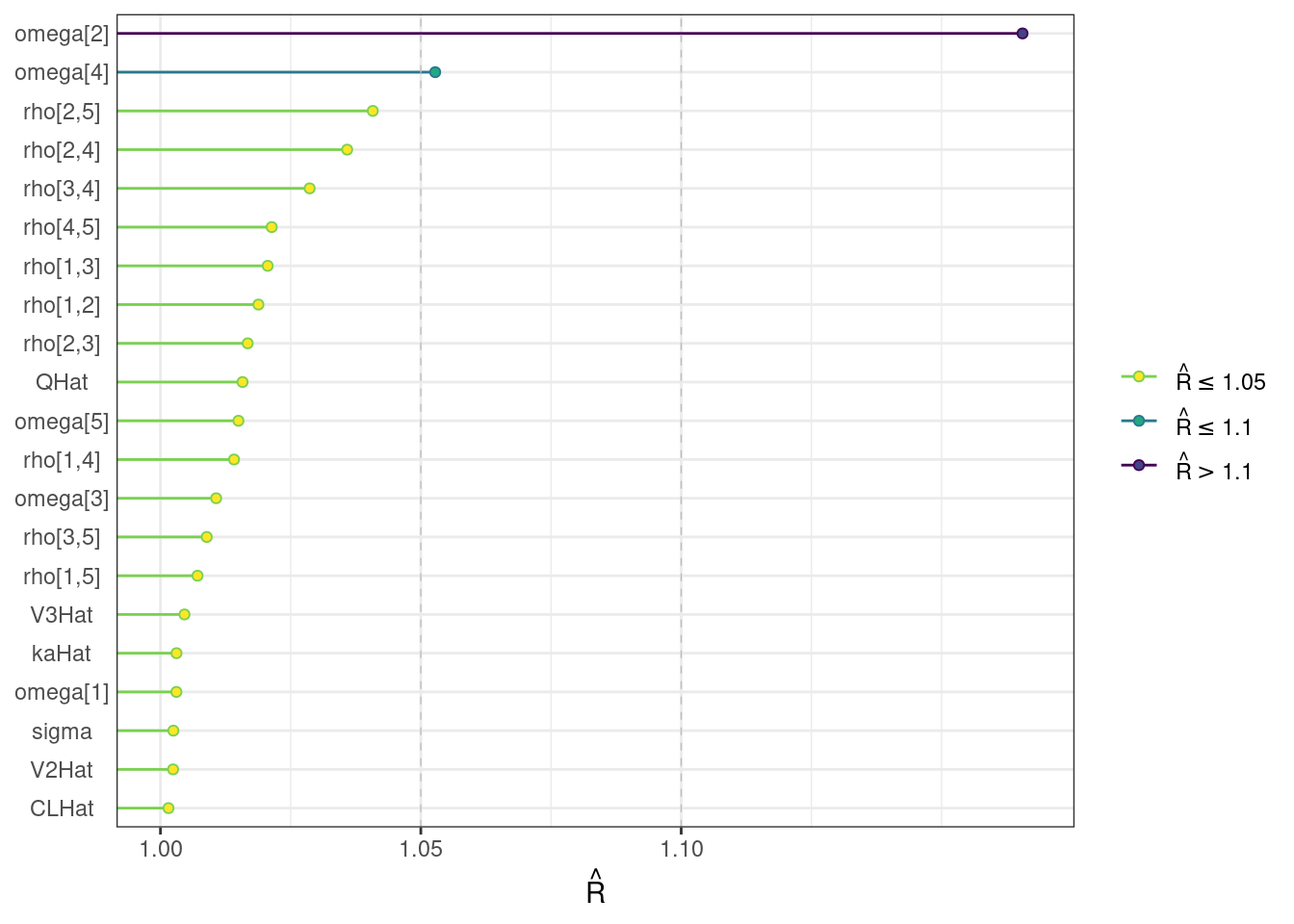

Figure 1: R-hat plot for model ppkexpo1.

ESS plots

We can also visualize the bulk and tail ESS as ratios of the effective sample size (Neff) to the total number of iterations (N).

ess_bulk <- draws_sum$ess_bulk
names(ess_bulk) <- draws_sum$variable
ess_bulk_ratios <- ess_bulk / (n_iter * n_chains)
ess_bulk_plot <- mcmc_neff(ess_bulk_ratios) + yaxis_text() +
  labs(title = "Bulk ESS ratios")
ess_bulk_plot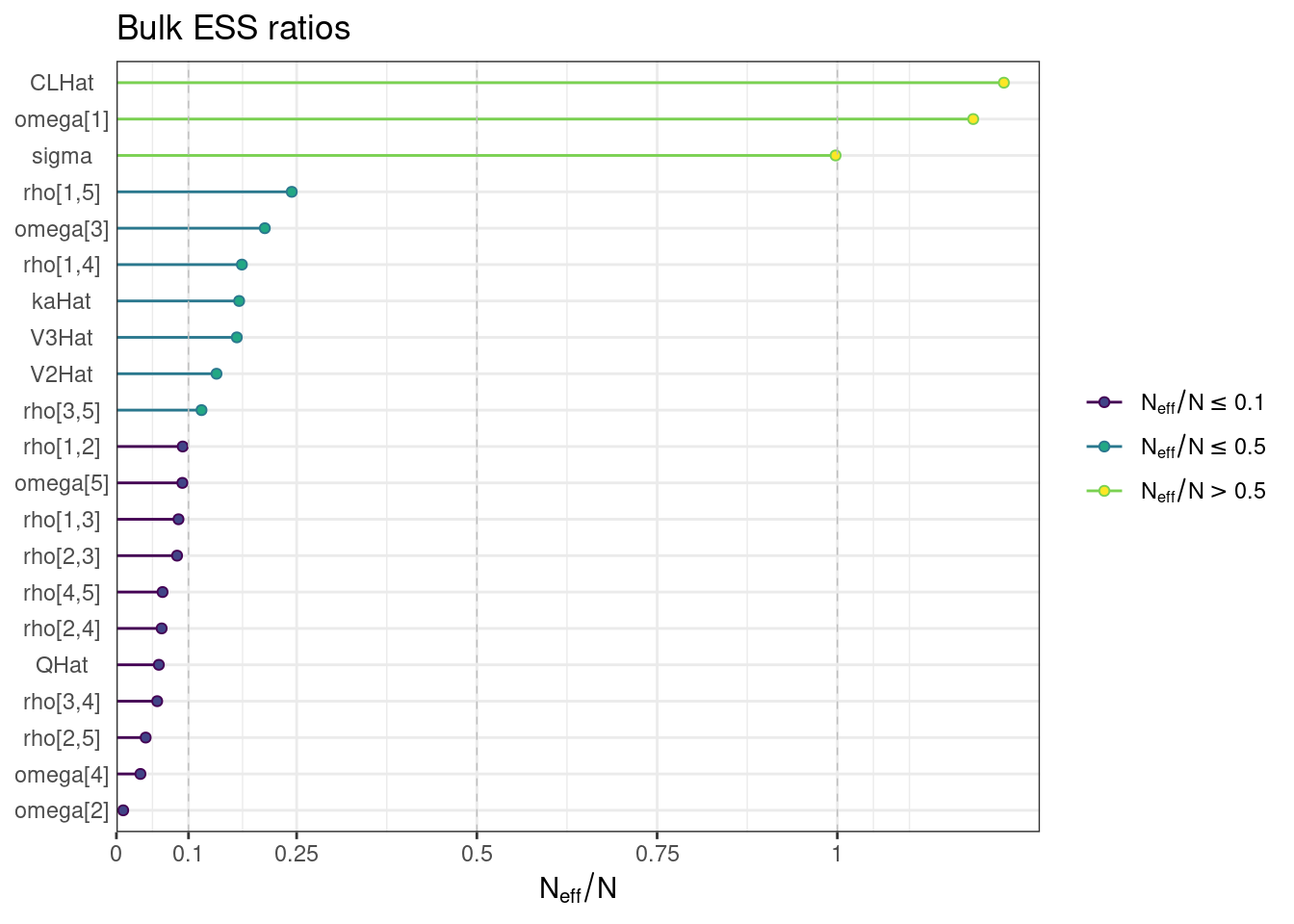

Figure 2: ESS bulk plot for model ppkexpo1.
ess_tail <- draws_sum$ess_tail
names(ess_tail) <- draws_sum$variable
ess_tail_ratios <- ess_tail / (n_iter * n_chains)
ess_tail_plot <- mcmc_neff(ess_tail_ratios) + yaxis_text() +
  labs(title = "Tail ESS ratios")
ess_tail_plot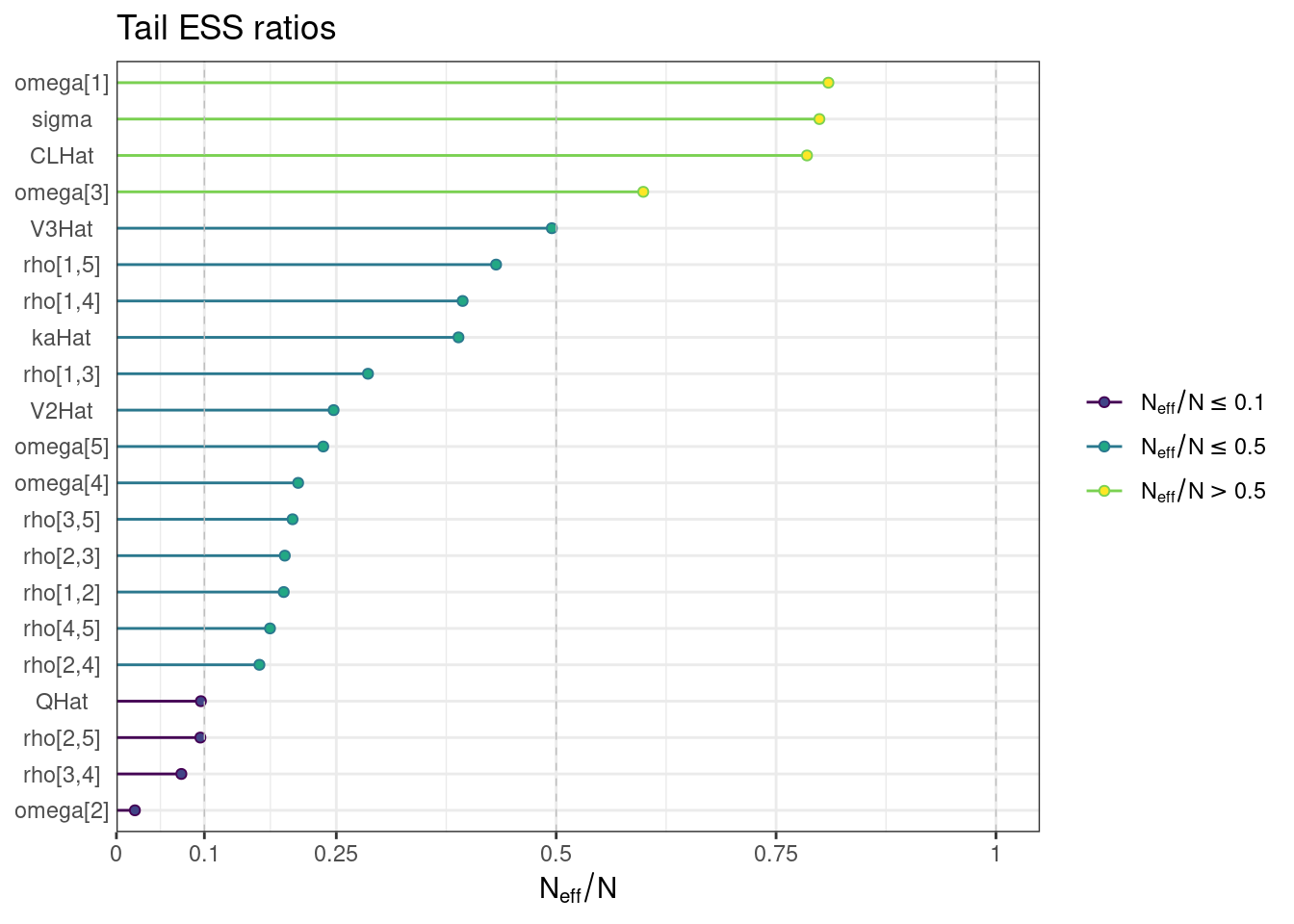

Figure 3: ESS tail plot for model ppkexpo1.

Trace and density plots

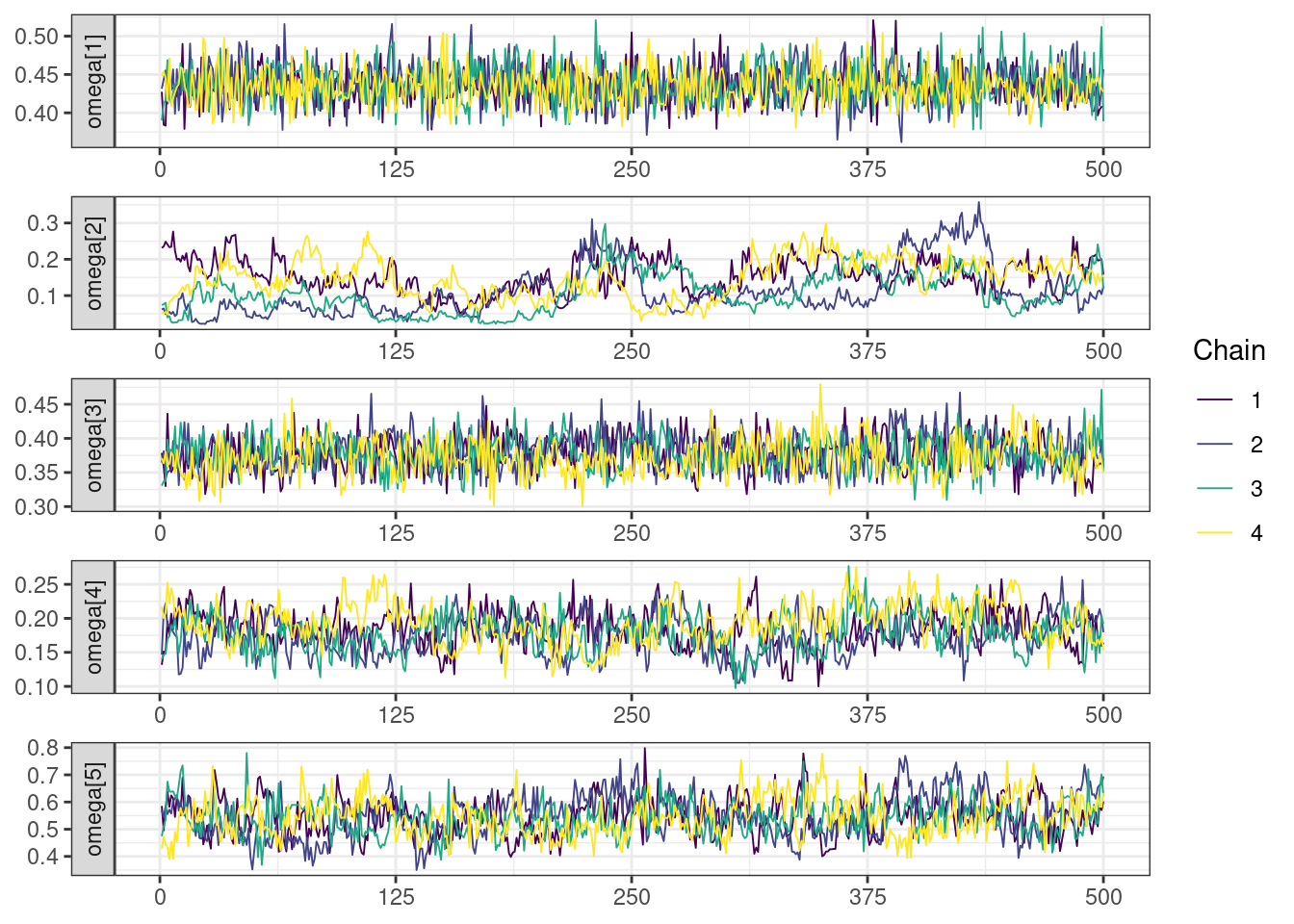
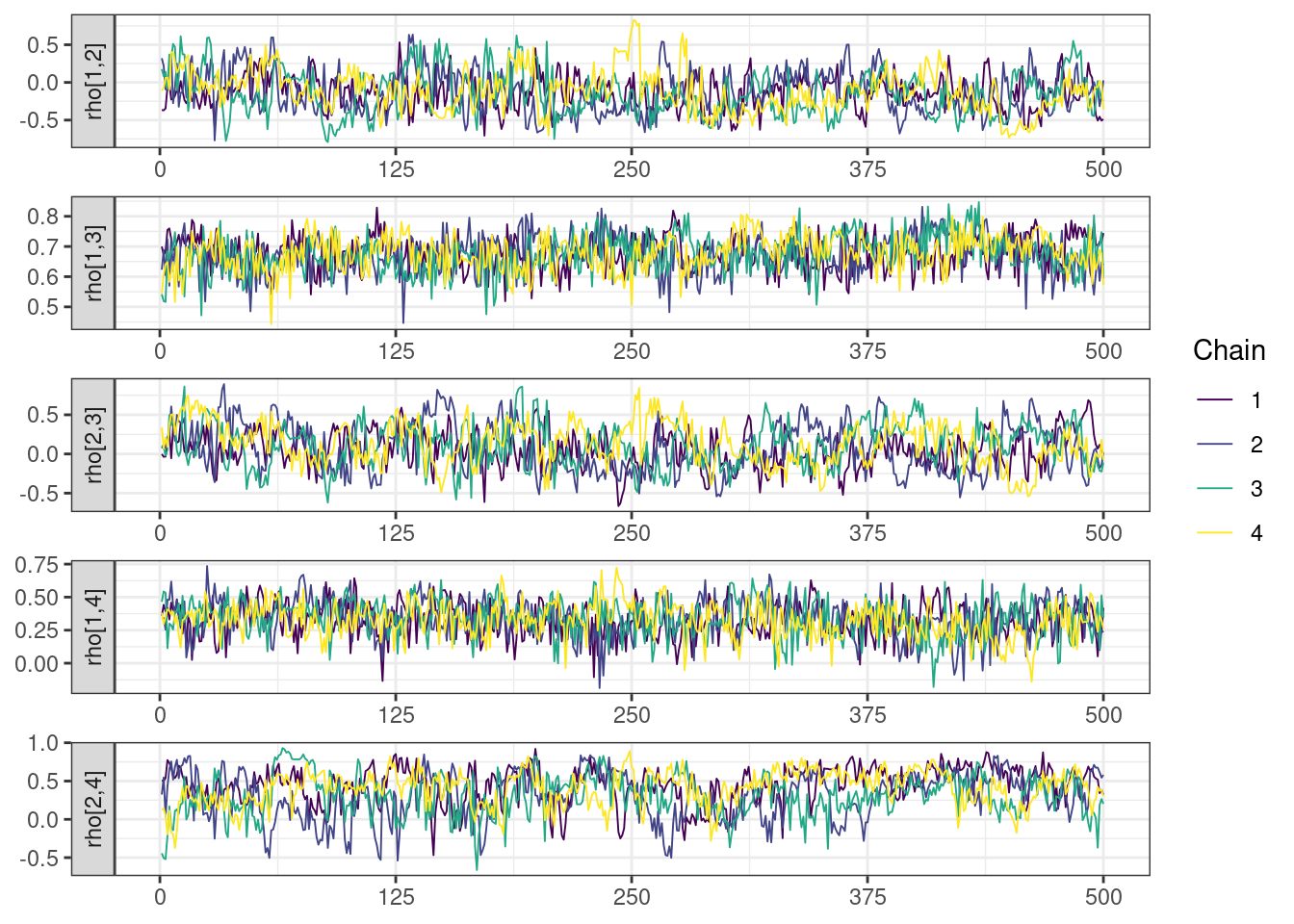
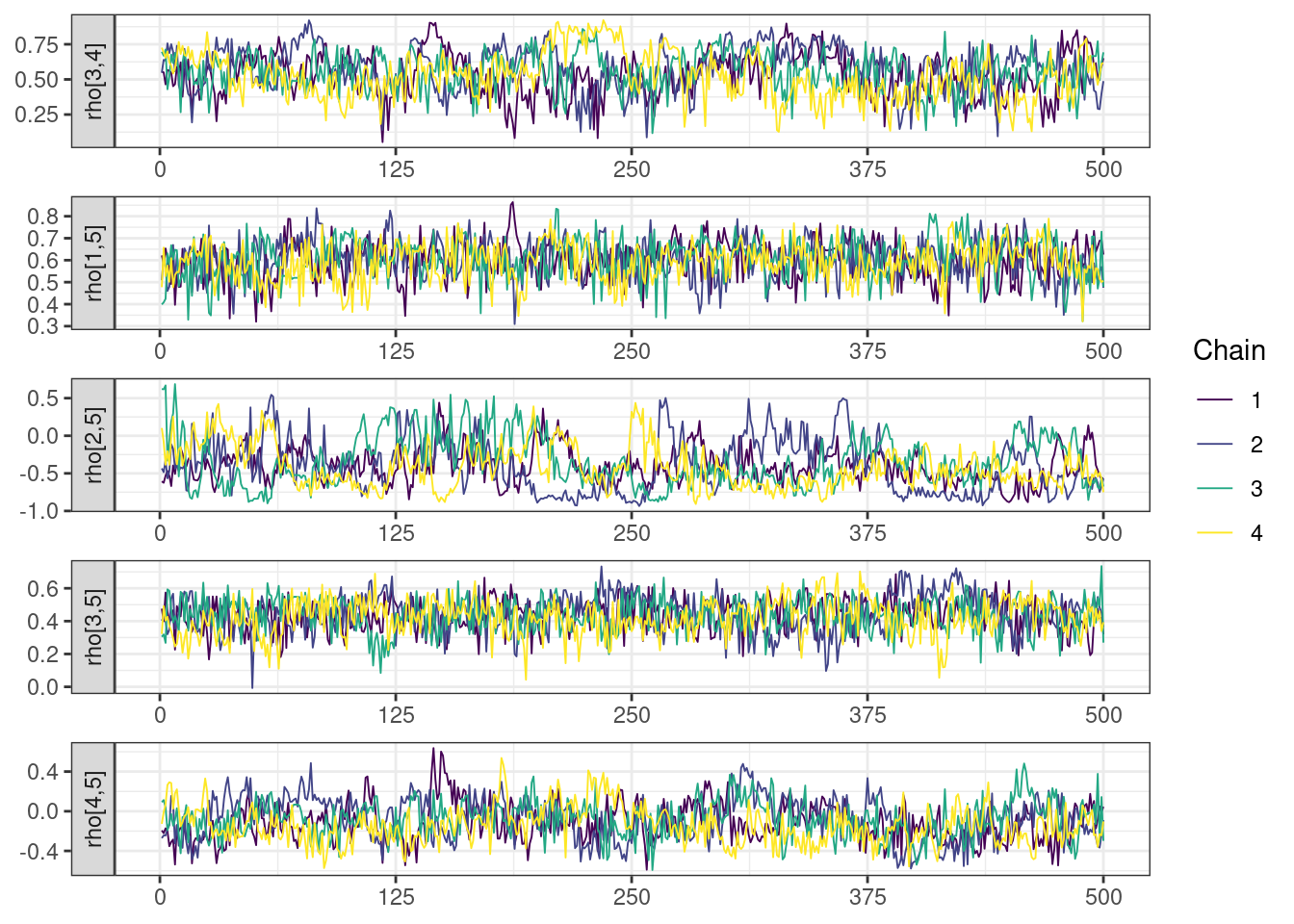
Next, we look at the trace and density plots.

mcmc_history_plots <- mcmc_history(posterior,
                                  nParPerPage = 6, 
                                  np = np)
mcmc_history_plots
. [[1]]
. 
. [[2]]
. 
. [[3]]
. 
. [[4]]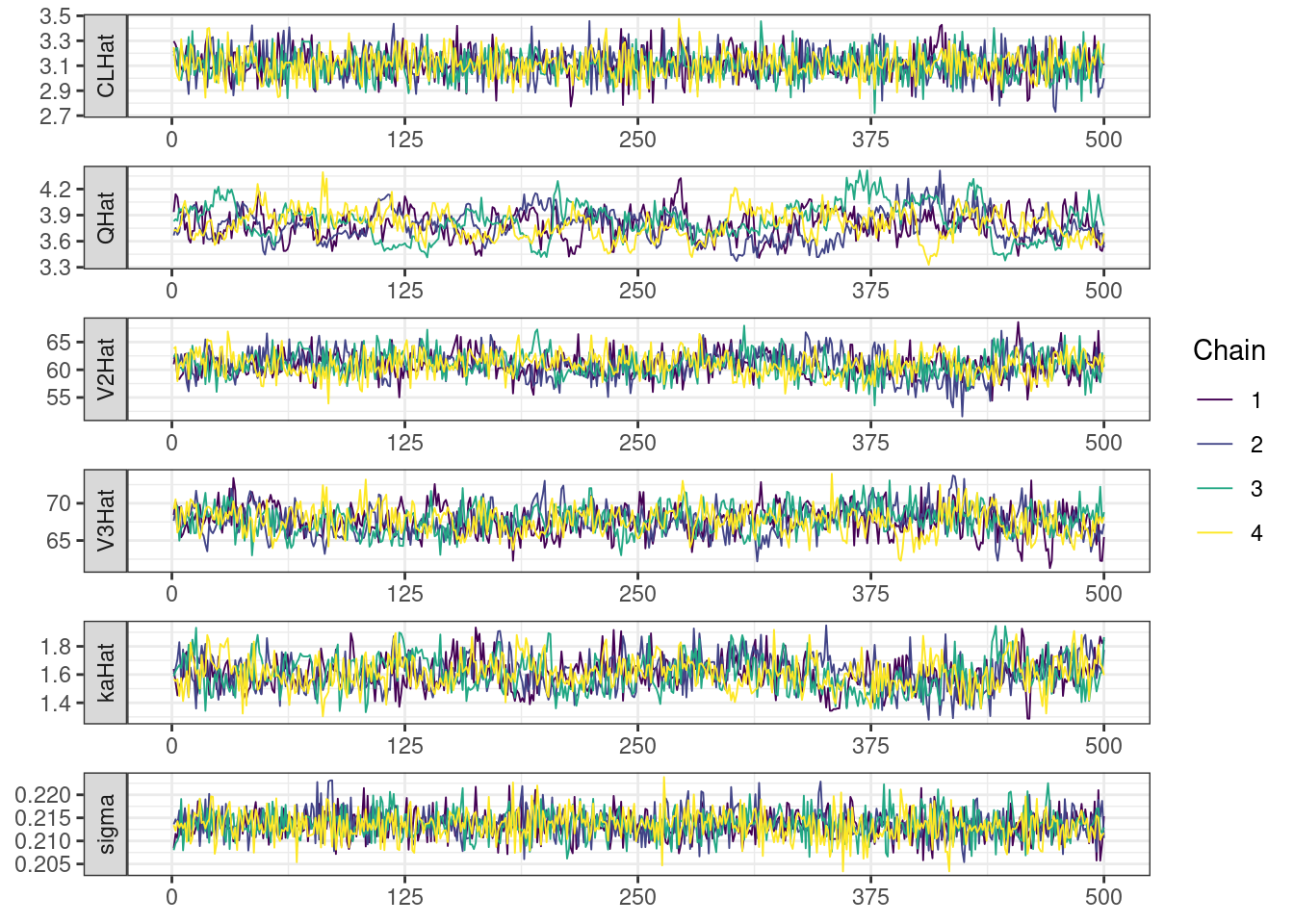

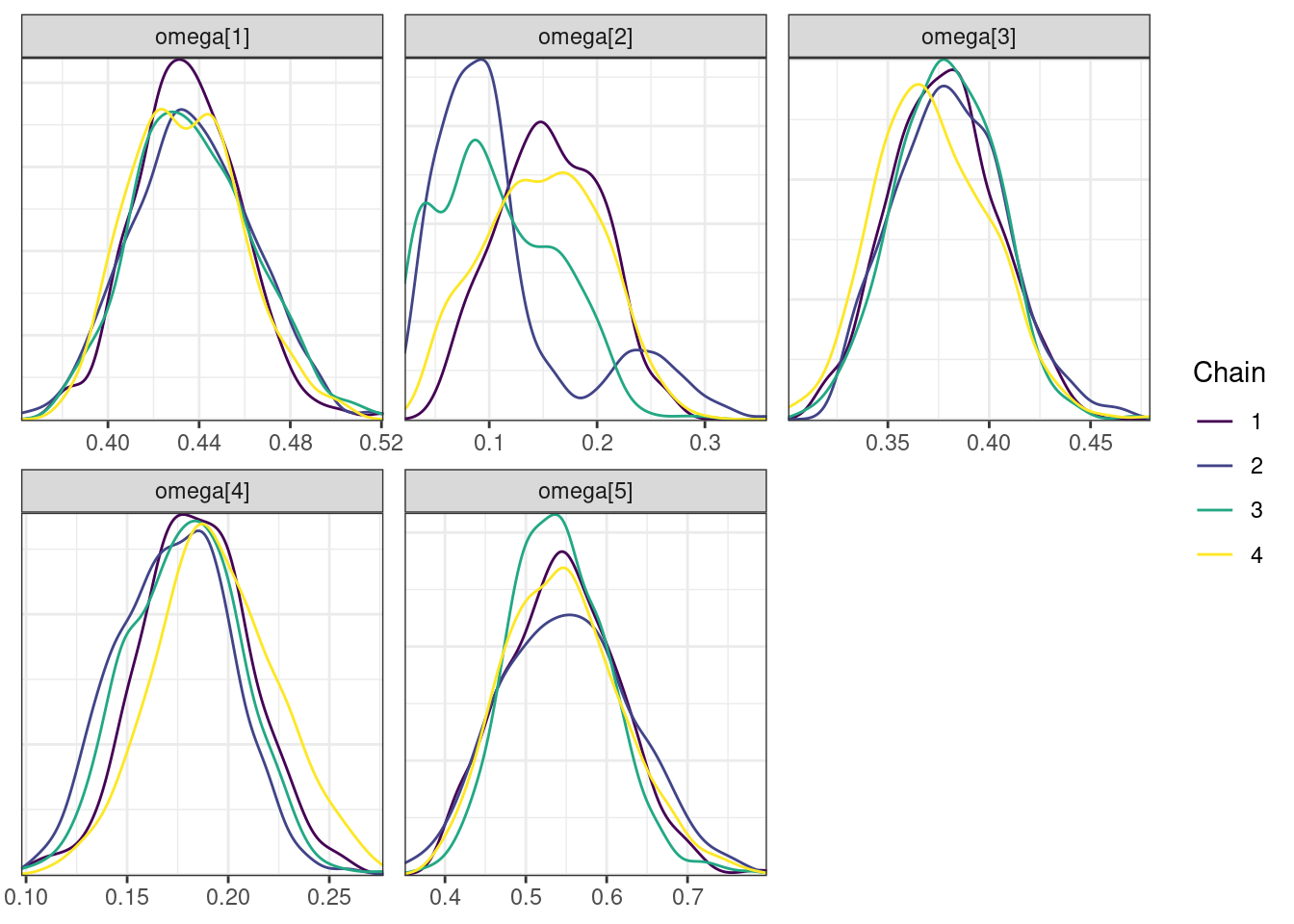
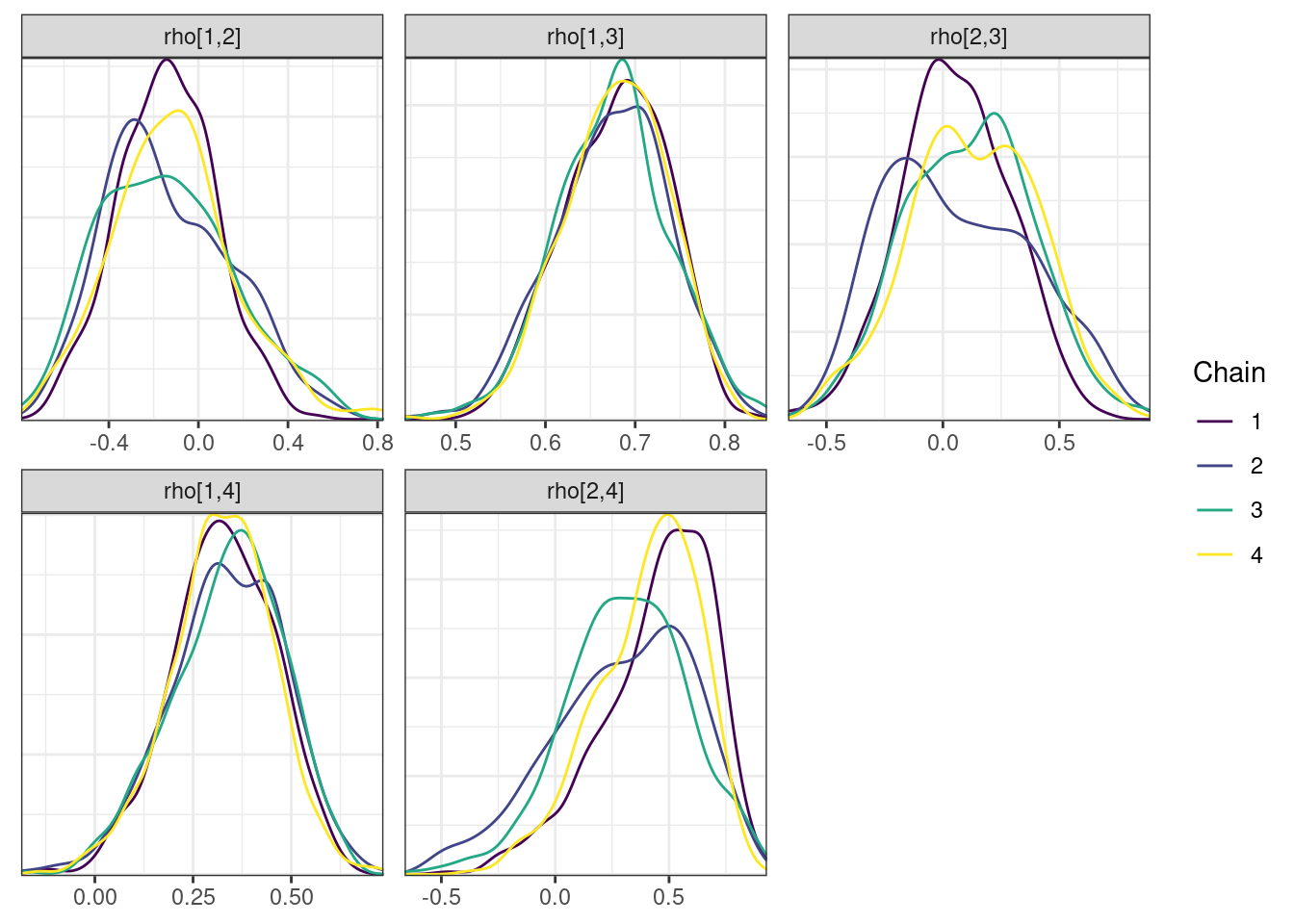
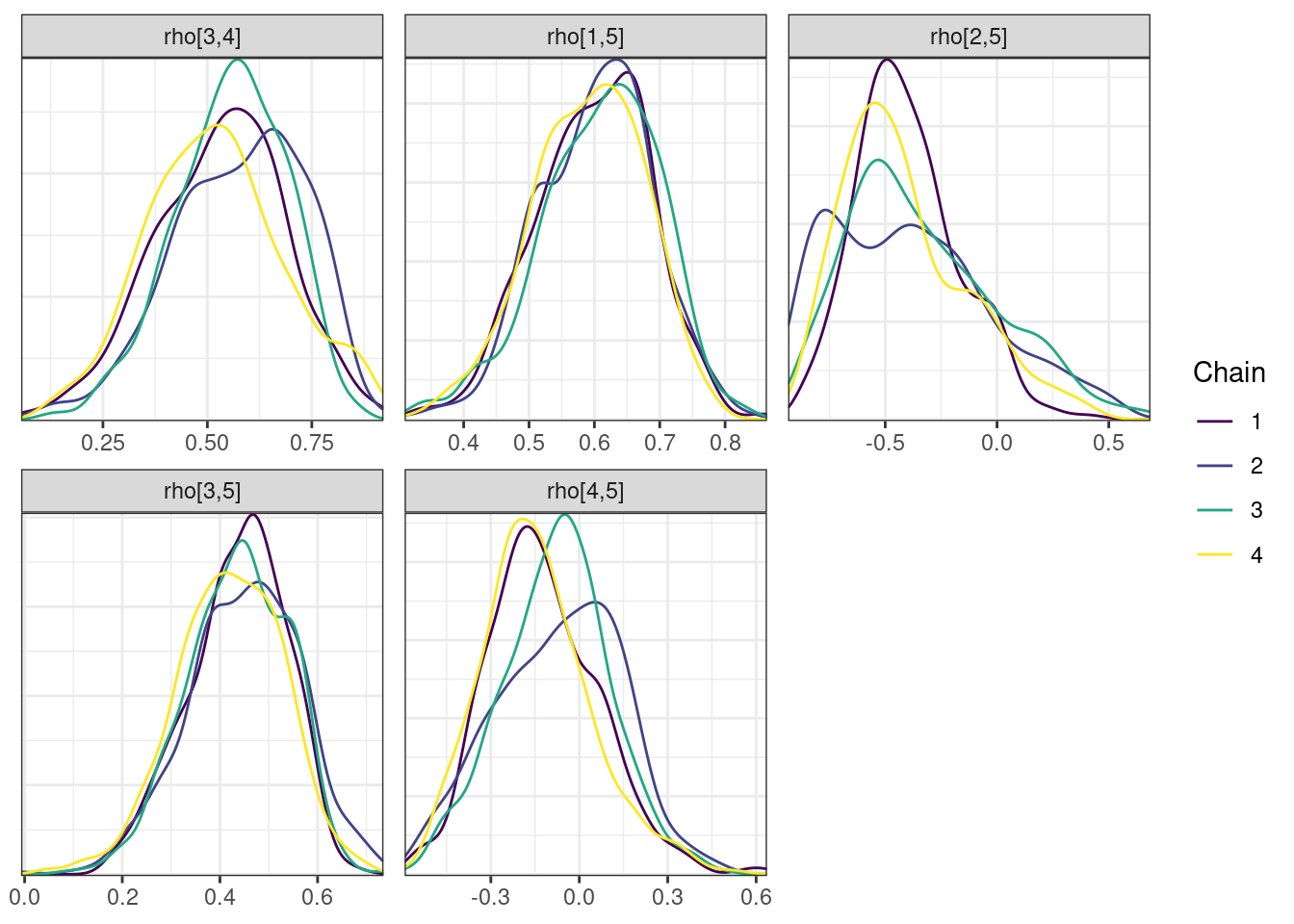
Figure 4: MCMC trace plots for model ppkexpo1.

Figure 5: MCMC trace plots for model ppkexpo1.

Figure 6: MCMC trace plots for model ppkexpo1.

Figure 7: MCMC trace plots for model ppkexpo1.
  mcmc_density_chain_plots <- mcmc_density(posterior, 
                                           nParPerPage = 6, byChain = TRUE)
mcmc_density_chain_plots
. [[1]]
. 
. [[2]]
. 
. [[3]]
. 
. [[4]]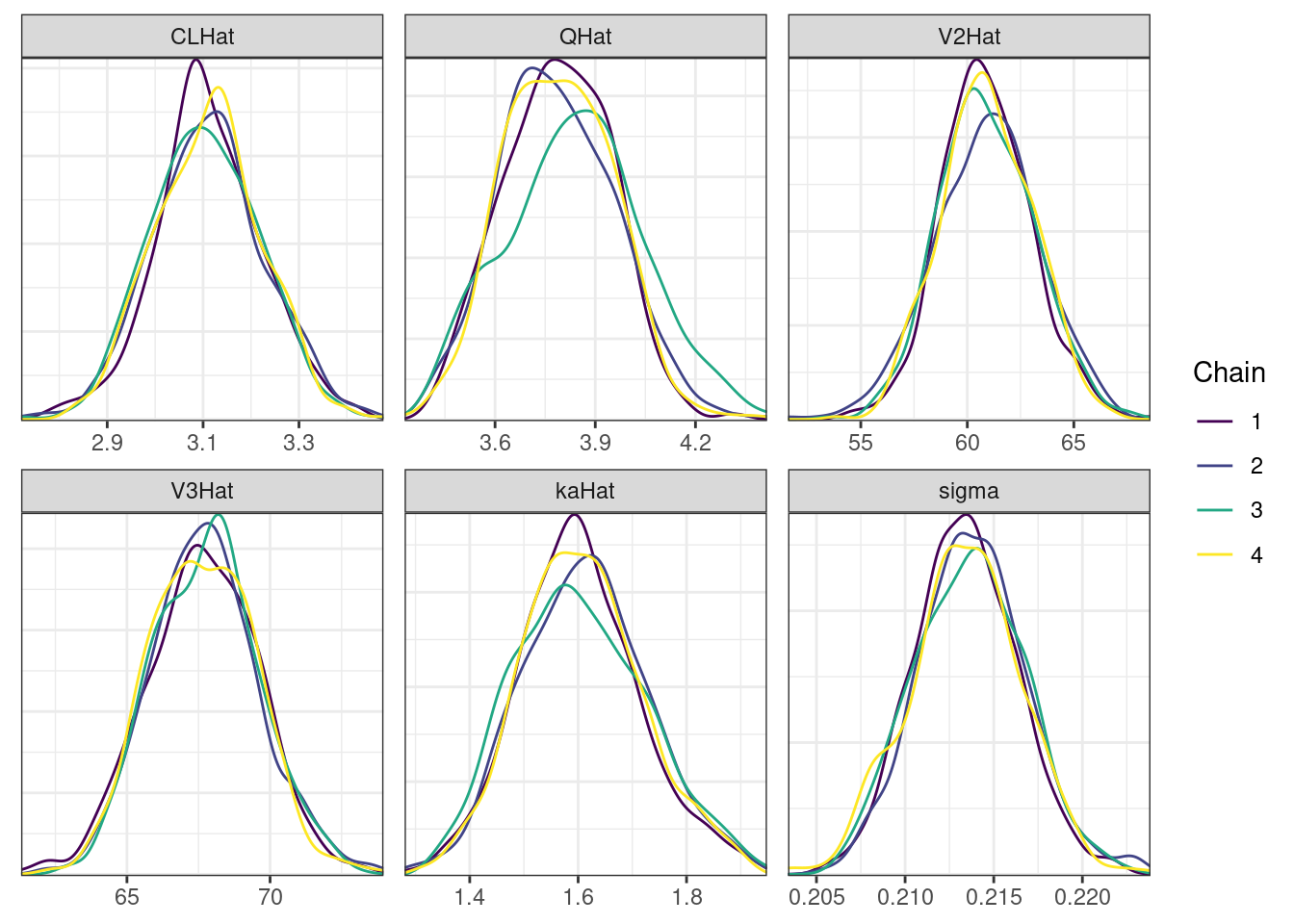

Figure 8: MCMC density plots for model ppkexpo1.

Figure 9: MCMC density plots for model ppkexpo1.

Figure 10: MCMC density plots for model ppkexpo1.

Figure 11: MCMC density plots for model ppkexpo1.

A scatterplot of the MCMC draws can be useful in showing bivariate relationships in the posterior distribution. The default scatterplot generated with mcmc_pairs uses points for the off-diagonal panels and histograms along the diagonal. We restrict this plot to only CLHat, QHat, V2Hat, V3Hat, kaHat, and sigma.

pairs_plot <- mcmc_pairs(posterior, pars = pars[!(grepl("rho", pars) | grepl("omega", pars))])
pairs_plot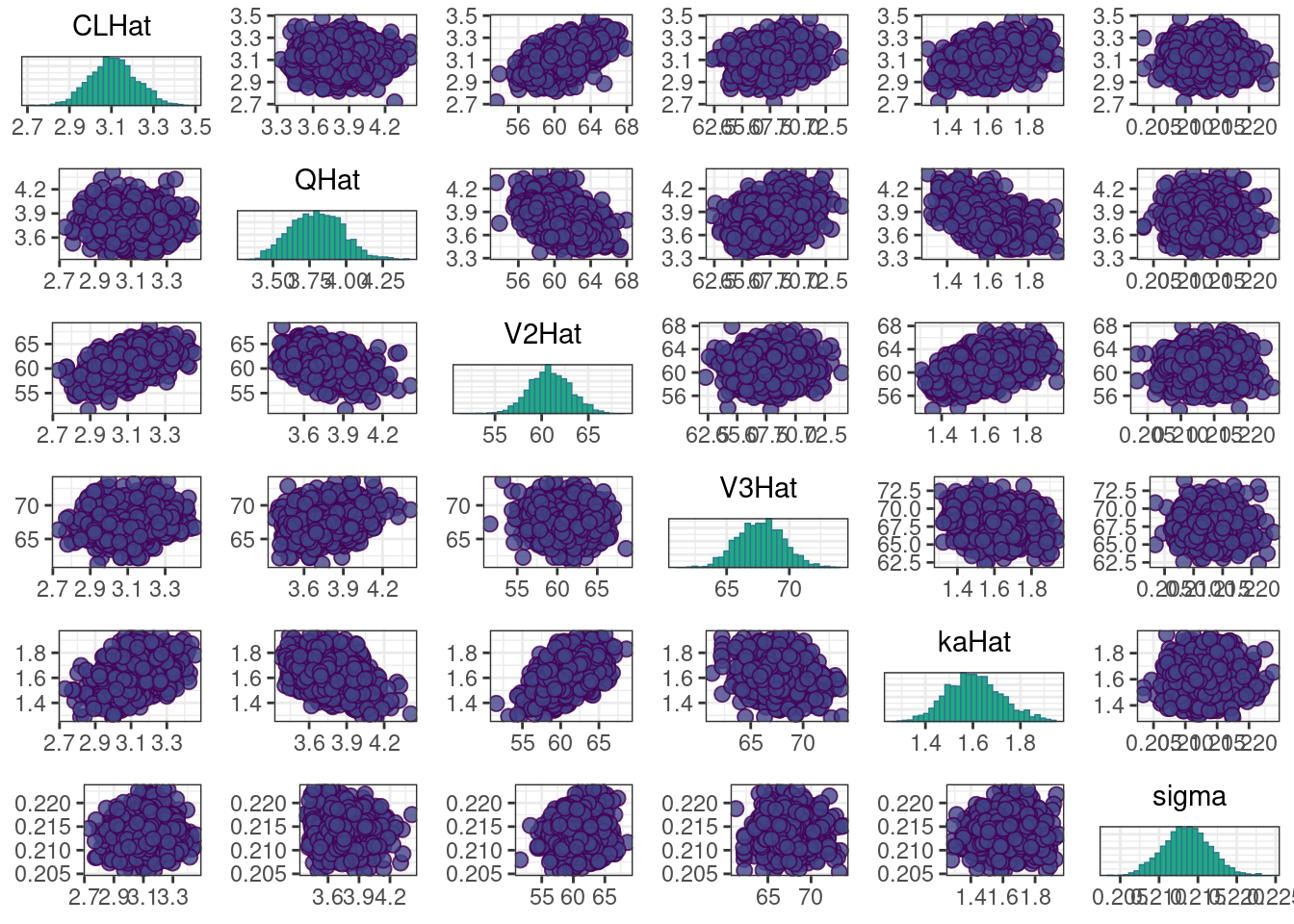

Figure 12: Plots of bivariate distributions of model parameters, a.k.a., pairs plots.

A more informative plot might use density estimates and transformations to bounded parameters. We can make these modifications using the diag_fun, off_diag_fun, and transformations arguments:

pairs_plot2 <- mcmc_pairs(posterior, 
           pars = pars[!(grepl("rho", pars) | grepl("omega",
                                                           pars))],
           transformations = "log",
           diag_fun = 'dens',
           off_diag_fun = 'hex')
pairs_plot2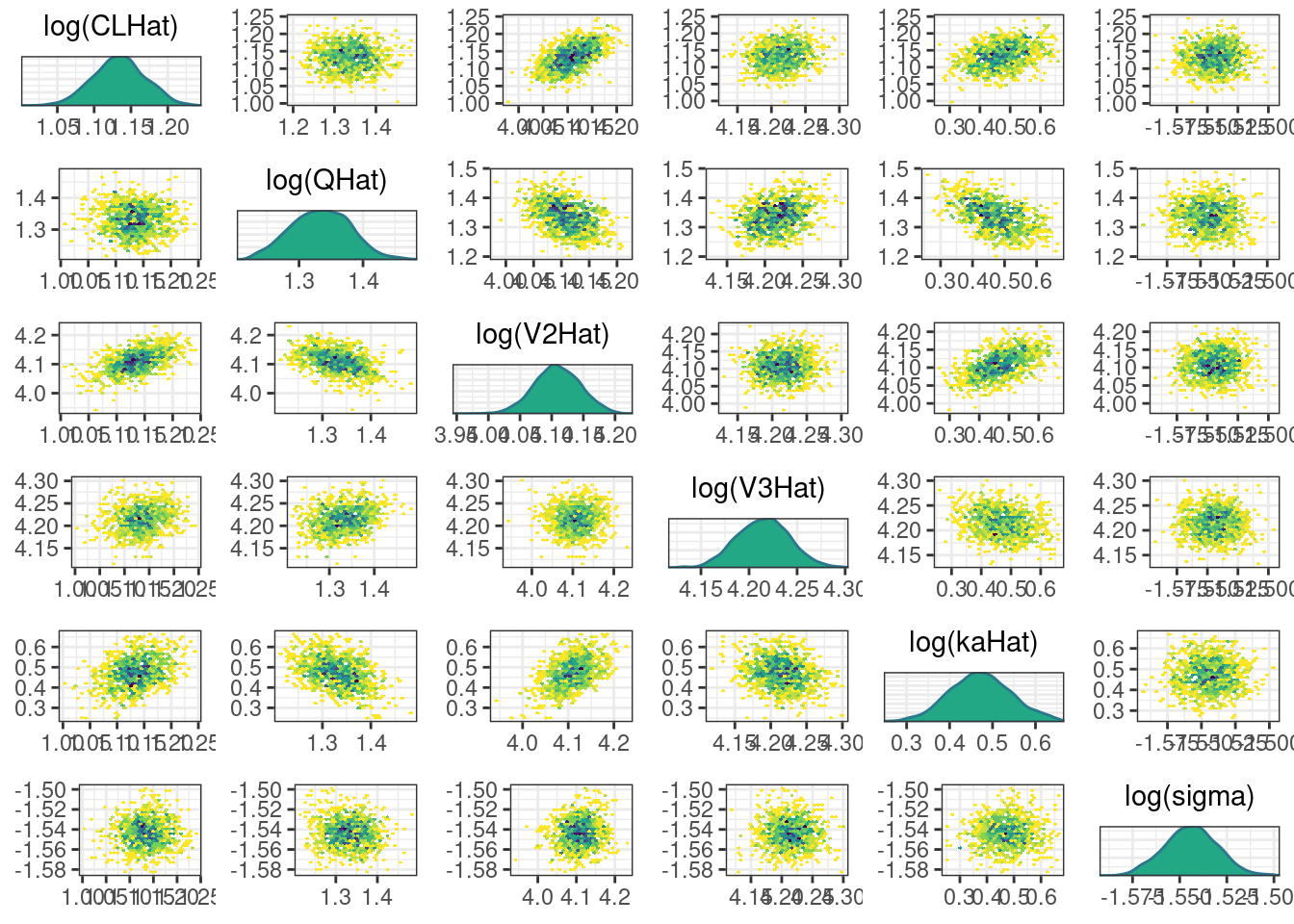

Figure 13: Plots of bivariate distributions of model parameters, a.k.a., pairs plots.

While most MCMC diagnostics look reasonably good, omega[2] is a notable exception as shown by a large Rhat, low effective sample sizes, a “wiggly snake” trace plot, and density plots indicating differences among the chains. The small number of divergent transitions, while not serious, suggests we should consider some intervention. The next logical steps are to increase the number of MCMC iterations, or reparameterize, to improve sampling performance (or both).

Other resources

The following script from the GitHub repository is discussed on this page. If you’re interested running this code, visit the About the GitHub Repo page first.

MCMC Diagnostics script: mcmc-diagnostics.Rmd

More details on the visual MCMC diagnostics are available in a Vignettes from bayesplot package developers.